题目内容
数列{an}满足
，若
，则a2004的值为 ．
【答案】分析：先根据递推关系式求出a2、a3、a4的值，可发现数列{an}是以3为周期的数列，再由2004=3×668得到a2004=a3可得到答案．
解答：解：∵
，
，
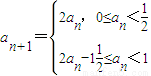∴a2=2×a1-1=
，
，
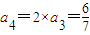
∴数列{an}是以3为周期的数列
∵2004=3×668∴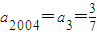
故答案为：
点评：本题主要考查数列的递推关系式，属基础题．
解答：解：∵
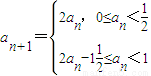，，∴a2=2×a1-1=
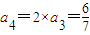
，，∴数列{an}是以3为周期的数列
∵2004=3×668∴
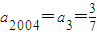
故答案为：
点评：本题主要考查数列的递推关系式，属基础题．
练习册系列答案
相关题目
，若对一切n∈N+都有an+1＞an，则a1的取值范围是 ．