Question

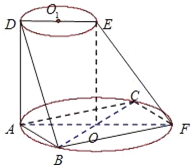如图所示，AF、DE分别是⊙O、⊙O₁的直径，AD与两圆所在的平面均垂直，AD=8．BC是⊙O的直径，AB=AC=6，OE∥AD．
（Ⅰ）求二面角B-AD-F的大小；
（Ⅱ）求直线BD与EF所成的角．

Answer 1

分析：（Ⅰ）由AD与两圆所在的平面均垂直，则AD⊥AB，AD⊥AF，故∠BAF是二面角B-AD-F的平面角，解三角形∠BAF即可得到结论．
（Ⅱ）以O为原点，BC、AF、OE所在直线为坐标轴，建立空间直角坐标系，我们易给出图象中相应点的坐标，进而利用空间向量法解答，即BD与EF所成的角的余弦值，等于空间向量

BD

与

EF

夹角余弦值的绝对值．

解答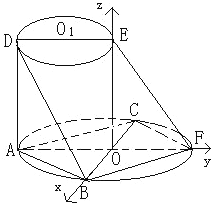：解：（Ⅰ）∵AD与两圆所在的平面均垂直，
∴AD⊥AB，AD⊥AF，故∠BAF是二面角B-AD-F的平面角，
依题意可知，ABCF是正方形，所以∠BAF=45°．
即二面角B-AD-F的大小为45⁰；
（Ⅱ）以O为原点，BC、AF、OE所在直线为坐标轴，
建立空间直角坐标系（如图所示），
则O（0，0，0），A（0，-3

2

，0），B（3

2

，0，0），
D（0，-3

2

，8），E（0，0，8），F（0，3

2

，0）
所以，

BD

=(-3

2

，-3

2

，8)，

FE

=(0，-3

2

，8)
cos＜

BD

，

EF

＞=

BD • FE

| BD || FE |

=

0+18+64

100 × 82

=

82

10

设异面直线BD与EF所成角为α，
则α=arccos

82

10

则直线BD与EF所成的角为arccos

82

10

点评：空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值；
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值；
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值；