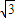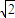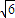题目内容
已知双曲线E的离心率为e，左、右两焦点分别为F1、F2，抛物线C以F2为顶点，F1为焦点，点P为抛物线与双曲线右支上的一个交点，若a|PF2|+c|PF1|=8a2，则e的值为（ ）
A、
| ||
| B、3 | ||
C、
| ||
D、
|
分析：作出图象，结合图象知抛物线准线的方程为x=3c，根据抛物线的定义可得|PF1|=|PR|=3c-x0，
根据双曲线的第二定义可得
=e，由已知a|PF2|+c|PF1|=8a2，可得e=
．
根据双曲线的第二定义可得
| |PF2| | ||
x0-
|
| 3 |
解答：
解：如右图所示，设点P的坐标为（x0，y0），由抛物线以F2为顶点，F1为焦点，可得其准线的方程为x=3c，根据抛物线的定义可得|PF1|=|PR|=3c-x0，又由点P为双曲线上的点，根据双曲线的第二定义可得
=e，即得|PF2|=ex0-a，由已知a|PF2|+c|PF1|=8a2，可得-a2+3c2=8a2，即e2=3，由e＞1可得e=
，
故选A．
解：如右图所示，设点P的坐标为（x0，y0），由抛物线以F2为顶点，F1为焦点，可得其准线的方程为x=3c，根据抛物线的定义可得|PF1|=|PR|=3c-x0，又由点P为双曲线上的点，根据双曲线的第二定义可得| |PF2| | ||
x0-
|
| 3 |
故选A．
点评：本题考查双曲线的性质和应用，解题时要结合题设条件，作出图象，数形结合进行求解．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
学科网
学科网
