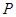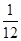题目内容
(本题满分14分)一个袋中装有大小和质地都相同的10个球,其中黑球4个,白球5个,红球1个。
(1)从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的概率分布和数学期望E(X);
(2)每次从袋中随机地摸出一球,记下颜色后放回.求3次摸球后,摸到黑球的次数大于摸到白球的次数的概率。
(1)分布列是:
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
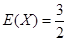
(2)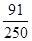
【解析】
试题分析:(1)由题意知随机变量X的取值为0,1,2,3,所以分布列是
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
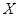 的数学期望是
的数学期望是 .
-----7分
.
-----7分
(2)记3次摸球中,摸到黑球次数大于摸到白球次数为事件A,
则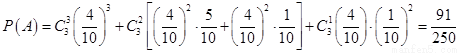
答:摸到黑球的次数大于摸到白球的次数的概率为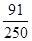 .
-----14分
.
-----14分
考点:本小题主要考查离散型随机变量及其分布列、数学期望、n次独立重复试验的概率的计算,考查学生的逻辑推理能力,理解问题、分析问题、解决问题的能力及分类讨论思想的应用.
点评:解决此类问题要注意判准事件的性质,根据事件的性质识别概率模型,能否正确列出
分布列将直接影响数学期望的求解.求解过程中要注意概率表示方法的一致性,题目中用小
数表示的都是小数,用分数表示的都是分数.

(本题满分14分) 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值.
(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.