题目内容
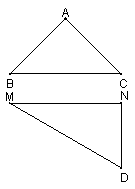
(本题满分14分)一副三角板(如答卷图),其中![]() 中,AB=AC,
中,AB=AC,![]() ,
,![]() 中,
中,![]() ,
,![]() ,现将两相等长的边BC、MN重合,并翻折构成四面体ABC D.
,现将两相等长的边BC、MN重合,并翻折构成四面体ABC D.![]()
(1)当平面ABC![]() 平面BCD(图(1))时,求直线AD与平面BCD所成角的正弦值;
平面BCD(图(1))时,求直线AD与平面BCD所成角的正弦值;
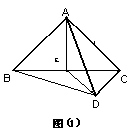
(2)当将平面ABC翻折到使A到B、C、D三点的距离相等时(图(2)),
①求证:A在平面BCD内的射影是BD的中点;
②求二面角A-CD-B的余弦值.
(本小题满分14分)
 解:(1)过A作AE
解:(1)过A作AE![]() BC于E,连ED,
BC于E,连ED,![]() 面ABC
面ABC![]() 面BCD,
面BCD, ![]()
![]() 就是AD与面BCD所成的角----------2分
就是AD与面BCD所成的角----------2分
∵DC=![]() ,则BC=
,则BC=![]() ,AE=
,AE=![]() ,DE=
,DE=![]()
![]() ,
,![]()
即AD与面BCD所成角的正弦值为![]() .----------5分
.----------5分
(2)①设A在平面BCD内的射影为O,连OB、OC、OD,![]()

![]() ,
,
![]()
![]() 是
是![]() 的外心,即BD边的中 点.-----------9分
的外心,即BD边的中 点.-----------9分
②取CD中点F,连OF、AF,由①得A在面BCD内的射影为O,
OF∥BC,∴ OF⊥CD,∴AF⊥CD,
∴∠AFO就是二面角A-CD-B的平面角;-----------11分
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
又 ∵![]()
∴![]() ,∴
,∴![]() 中,
中,![]()
即二面角A-CD-B的余弦值为![]() ----------------14分
----------------14分

 口算题天天练系列答案
口算题天天练系列答案(本题满分14分) 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值.
(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.