Question

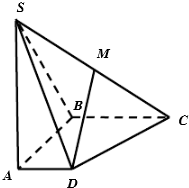如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD∥BC，SA⊥CD，AB⊥平面SAD，点M是SC的中点，且SA=AB=BC=1，AD=

1

2

．
（1）求四棱锥S-ABCD的体积；
（2）求证：DM∥平面SAB；
（3）求直线SC和平面SAB所成的角的正弦值．

Answer 1

分析：（1）先证明侧棱SA⊥底面ABCD，再求四棱锥S-ABCD的体积；
（2）取SB的中点N，证明四边形MNAD是平行四边形，利用线面平行的判定定理证明DM∥平面SAB；
（3）证明∠BSC是直线SC和平面SAB所成的角，在Rt△SBC中，即可求解．

解答：（1）解：∵AB⊥底面SAD，SA?底面SAD，AD?底面SAD
∴AB⊥SA，AB⊥AD
∵SA⊥CD，AB、CD是平面ABCD内的两条相交直线
∴侧棱SA⊥底面ABCD
∴四棱锥S-ABCD的体积为

1

3

×

1

2

×（

1

2

+1）×1×1=

1

4

；
（2）证明：取SB的中点N，则
∵点M是SC的中点，∴MN∥BC，MN=

1

2

BC
∵底面是直角梯形，BC=1，
∴AD∥BC且AD=

1

2

BC
∴MN∥AD且MN=AD
∴四边形MNAD是平行四边形
∴DM∥AN
∵DM?平面SAB，AN?平面SAB
∴DM∥平面SAB；
（3）解：∵侧棱SA⊥底面ABCD，BC?底面ABCD，∴BC⊥SA
∵AB⊥BC，AB、SA是平面SAB内的两条相交直线
∴BC⊥平面SAB，垂足是点B
∴SB是SC在平面SAB内的射影，BC⊥SB
∴∠BSC是直线SC和平面SAB所成的角
∵在Rt△SBC中，BC=1，SB=

2

，∴SC=

3

∴sin∠BSC=

BC

SC

=

3

3

∴直线SC和平面SAB所成的角的正弦值是

3

3

．

点评：本题考查四棱锥的体积，考查线面平行，考查线面角，考查学生分析解决问题的能力，属于中档题．