题目内容
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点(1)求证:EF∥平面SAD
(2)设SD=2CD,求二面角A-EF-D的大小.
分析:法一:(1)作FG∥DC交SD于点G,则G为SD的中点.
要证EF∥平面SAD,只需证明EF平行平面SAD内的直线AG即可.
(2)取AG中点H,连接DH,说明∠DMH为二面角A-EF-D的平面角,解三角形求二面角A-EF-D的大小.
法二:建立空间直角坐标系,
=
,EF∥AG,AG?平面SAD即可证明(1);
(2)求出向量
和
,利用cos<
,
>=
,即可解答本题.
要证EF∥平面SAD,只需证明EF平行平面SAD内的直线AG即可.
(2)取AG中点H,连接DH,说明∠DMH为二面角A-EF-D的平面角,解三角形求二面角A-EF-D的大小.
法二:建立空间直角坐标系,
| EF |
| AG |
(2)求出向量
| MD |
| EA |
| MD |
| EA |
| ||||
|
|
解答: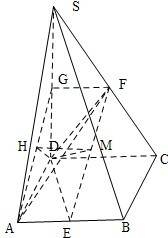 解:法一:
解:法一:
(1)作FG∥DC交SD于点G,则G为SD的中点.
连接AG,FG
CD,又CD
AB,
故FG
AE,AEFG为平行四边形.EF∥AG,又AG?平面SAD,EF?平面SAD.
所以EF∥平面SAD.
(2)不妨设DC=2,则SD=4,DG=2,△ADG为等
腰直角三角形.
取AG中点H,连接DH,则DH⊥AG.
又AB⊥平面SAD,所以AB⊥DH,而AB∩AG=A,
所以DH⊥面AEF.
取EF中点M,连接MH,则HM⊥EF.
连接DM,则DM⊥EF.
故∠DMH为二面角A-EF-D的平面角tan∠DMH=
=
=
.
所以二面角A-EF-D的大小为arctan
.
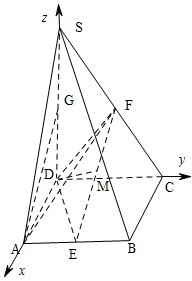
法二:(1)如图,建立空间直角坐标系D-xyz.
设A(a,0,0),S(0,0,b),则B(a,a,0),C(0,a,0),E(a,
,0),F(0,
,
),
=(-a,0,
).
取SD的中点G(0,0,
),则
=(-a,0,
).
=
,EF∥AG,AG?平面SAD,EF?平面SAD,
所以EF∥平面SAD.
(2)不妨设A(1,0,0),则B(1,1,0),C(0,1,0),S(0,0,2),E(1,
,0),F(0,
,1).EF中点M(
,
,
),
=(-
,-
,-
),
=(-1,0,1),
•
=0,MD⊥EF
又
=(0,-
,0),
•
=0,EA⊥EF,
所以向量
和
的夹角等于二面角A-EF-D的平面角.cos<
,
>=
=
.
所以二面角A-EF-D的大小为arccos
.
 解:法一:
解:法一:(1)作FG∥DC交SD于点G,则G为SD的中点.
连接AG,FG
| ||
. |
| 1 |
| 2 |
| ||
. |
故FG
| ||
. |
所以EF∥平面SAD.
(2)不妨设DC=2,则SD=4,DG=2,△ADG为等
腰直角三角形.
取AG中点H,连接DH,则DH⊥AG.
又AB⊥平面SAD,所以AB⊥DH,而AB∩AG=A,
所以DH⊥面AEF.
取EF中点M,连接MH,则HM⊥EF.
连接DM,则DM⊥EF.
故∠DMH为二面角A-EF-D的平面角tan∠DMH=
| DH |
| HM |
| ||
| 1 |
| 2 |
所以二面角A-EF-D的大小为arctan
| 2 |

法二:(1)如图,建立空间直角坐标系D-xyz.
设A(a,0,0),S(0,0,b),则B(a,a,0),C(0,a,0),E(a,
| a |
| 2 |
| a |
| 2 |
| b |
| 2 |
| EF |
| b |
| 2 |
取SD的中点G(0,0,
| b |
| 2 |
| AG |
| b |
| 2 |
| EF |
| AG |
所以EF∥平面SAD.
(2)不妨设A(1,0,0),则B(1,1,0),C(0,1,0),S(0,0,2),E(1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| MD |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| EF |
| MD |
| EF |
又
| EA |
| 1 |
| 2 |
| EA |
| EF |
所以向量
| MD |
| EA |
| MD |
| EA |
| ||||
|
|
| ||
| 3 |
所以二面角A-EF-D的大小为arccos
| ||
| 3 |
点评:半边天考查直线与平面平行的判定,二面角的求法,考查计算能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,