题目内容
当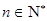 时,
时,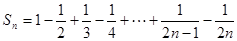
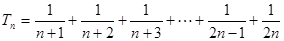
(1)求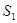 ,
,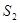 ,
,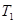 ,
,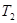 ;
;
(2)猜想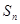 与
与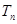 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.
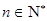 时,
时,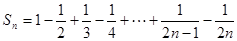
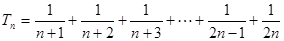
(1)求
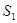 ,
,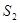 ,
,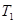 ,
,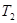 ;
;(2)猜想
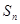 与
与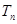 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.(1)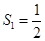 ,
,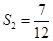
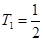
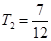
(2)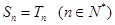 证明见解析
证明见解析
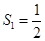 ,
,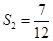
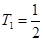
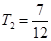
(2)
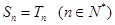 证明见解析
证明见解析(1)分别令n=1,n=2可求出S1,S2,T1,T2.
(2)根据(I)当中的结果,猜想出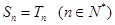 ,
,
因为是与正整数n有关的等式可以考虑采用数学归纳法证明.
再证明时一定要按两个步骤进行,缺一不可.
第一步,先验证:n=1时等式成立.
第二步,先假设n=k时,等式成立;再证明n=k+1时,等式也成立,但必须要用上n=k时,归纳假设,否则证明无效
(1)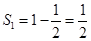 ,
,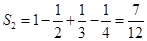
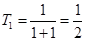
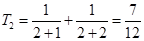 ………4分
………4分
(2)猜想: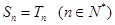 即:
即:
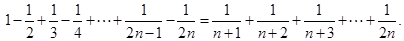 (n∈N*)6分
(n∈N*)6分
下面用数学归纳法证明
① n=1时,已证S1=T1 ………………7分
② 假设n=k时,Sk=Tk(k≥1,k∈N*),即:
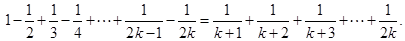 ……………9分
……………9分
则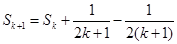
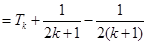 …11分
…11分
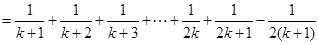
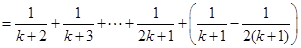
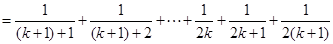
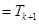
由①,②可知,对任意n∈N*,Sn=Tn都成立.
(2)根据(I)当中的结果,猜想出
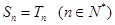 ,
,因为是与正整数n有关的等式可以考虑采用数学归纳法证明.
再证明时一定要按两个步骤进行,缺一不可.
第一步,先验证:n=1时等式成立.
第二步,先假设n=k时,等式成立;再证明n=k+1时,等式也成立,但必须要用上n=k时,归纳假设,否则证明无效
(1)
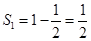 ,
,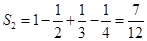
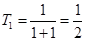
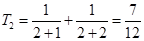 ………4分
………4分(2)猜想:
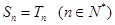 即:
即: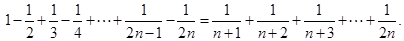 (n∈N*)6分
(n∈N*)6分下面用数学归纳法证明
① n=1时,已证S1=T1 ………………7分
② 假设n=k时,Sk=Tk(k≥1,k∈N*),即:
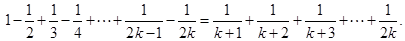 ……………9分
……………9分则
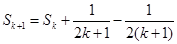
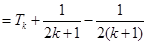 …11分
…11分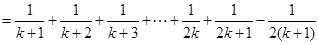
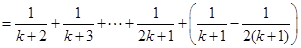
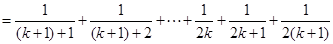
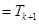
由①,②可知,对任意n∈N*,Sn=Tn都成立.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
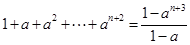 (
(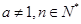 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为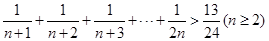 的过程中,
的过程中,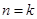 递推到
递推到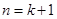 时的不等式左边( )
时的不等式左边( )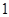 项
项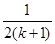
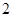 项
项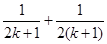
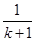 ”
”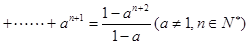 在验证n=1成立时,左边计算所得结果为 ( )
在验证n=1成立时,左边计算所得结果为 ( )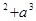
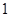 条线段,将圆分割成两部分;画
条线段,将圆分割成两部分;画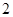 条相交线段,彼此分割成
条相交线段,彼此分割成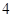 条线段,将圆分割成
条线段,将圆分割成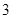 条线段,彼此最多分割成
条线段,彼此最多分割成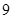 条线段,将圆最多分割成
条线段,将圆最多分割成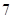 部分;画
部分;画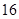 条线段,将圆最多分割成
条线段,将圆最多分割成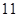 部分.
部分.


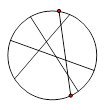
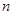 条线段,彼此最多分割成多少条线段?
条线段,彼此最多分割成多少条线段?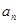 部分,归纳出
部分,归纳出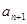 与
与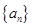 的通项公式,根据
的通项公式,根据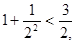 ,
,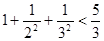 ,
, ……可归纳出式子为( )。
……可归纳出式子为( )。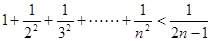
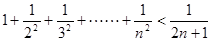
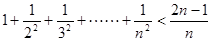
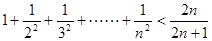
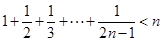
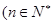 ,且
,且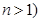 时,第一步应证明下述哪个不等式成立( )
时,第一步应证明下述哪个不等式成立( )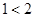
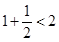
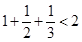
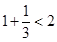
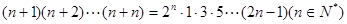 ”时,从
”时,从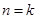 到
到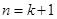 ,等式的左边需要增乘的代数式是__________ ;
,等式的左边需要增乘的代数式是__________ ;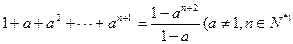 ,在验证当n=1时,等式
,在验证当n=1时,等式