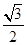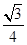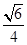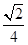题目内容
在△ABC中,a、b、c分别是角A、B、C的对边,且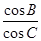 =-
=-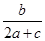 .
.
(1)求角B的大小;
(2)若b=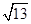 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
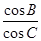 =-
=-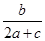 .
. (1)求角B的大小;
(2)若b=
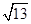 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.(1)B=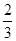 π.
π.
(2)S△ABC=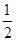 acsin B=
acsin B=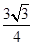 .
.
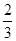 π.
π.(2)S△ABC=
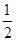 acsin B=
acsin B=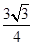 .
.此题考查了正弦定理,余弦定理及三角函数的恒等变形.熟练掌握定理及公式是解本题的关键.利用正弦定理表示出a,b及c是第一问的突破点.
(1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;
(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出b2,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值
(1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;
(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出b2,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值

练习册系列答案
相关题目
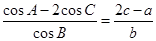 。
。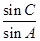 的值;
的值;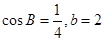 ,求
,求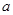 和
和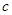 。
。 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是  ,且
,且 ="2,"
="2,"  .
. 的值.
的值. =3,求b,c的值.
=3,求b,c的值. 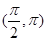



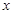 千米后,向右转
千米后,向右转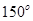 并走3千米,结果他离出发点恰好
并走3千米,结果他离出发点恰好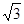 千米,那么
千米,那么 中,角
中,角 为锐角,记角
为锐角,记角 所对的边分别为
所对的边分别为 ,设向量
,设向量 ,且
,且 的夹角为
的夹角为
 的值及角
的值及角 ,求
,求 .
.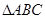 中,角
中,角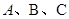 所对的边分别为
所对的边分别为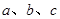 ,且
,且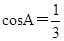 ,(1)求
,(1)求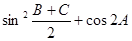 的值; (2)若
的值; (2)若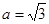 ,求
,求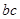 的最大值。
的最大值。 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 与
与 .现测得
.现测得 ,并在点
,并在点 的仰角为
的仰角为 ,求塔高
,求塔高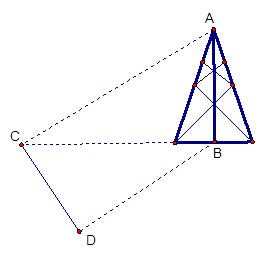
 ∠
∠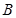 =
=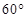 ,则△ABC的面积等于
,则△ABC的面积等于