题目内容
【题目】已知圆C的圆心在直线l:2x﹣y=0上,且与直线l1:x﹣y+1=0相切.
(Ⅰ)若圆C与圆x2+y2﹣2x﹣4y﹣76=0外切,试求圆C的半径;
(Ⅱ)满足已知条件的圆显然不只一个,但它们都与直线l1相切,我们称l1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.
【答案】(Ⅰ)![]() 1;(Ⅱ)还存在一条公切线,其方程为7x﹣y+5=0.
1;(Ⅱ)还存在一条公切线,其方程为7x﹣y+5=0.
【解析】
(I)设出圆![]() 的圆心坐标,利用圆心到直线
的圆心坐标,利用圆心到直线![]() 的距离表示半径,再根据两圆外切的条件列方程,解方程求得圆
的距离表示半径,再根据两圆外切的条件列方程,解方程求得圆![]() 的半径.
的半径.
(II)将另一条公切线的斜率分成存在和不存在两种情况进行分类讨论,结合圆心到两条公切线的距离相等列方程,由此求得另一条公切线的方程.
(Ⅰ)设圆C的圆心坐标为(a,2a),则半径r![]() ,
,
两圆的连心线长为![]() |a﹣1|
|a﹣1|![]() r,
r,
因为两圆外切,所以![]() r=r+9,∴r
r=r+9,∴r![]() 1;
1;
(Ⅱ)如果存在另一条切线,则它必过l与l1的交点(1,2),
①若斜率不存在,则直线方程为:x=1,圆心C到它的距离|a﹣1|=r![]() ,
,
由于方程需要对任意的a都成立,因此无解,所以它不是公切线,
②若斜率存在,设公切线方程为:y﹣2=k(x﹣1),
则d![]() r
r![]() 对任意的a都成立,
对任意的a都成立,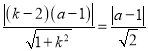 ,
,![]() ,两边平方并化简得k2﹣8k+7=0,解得k=1或k=7,
,两边平方并化简得k2﹣8k+7=0,解得k=1或k=7,
当k=1时,直线与l1重合,
当k=7时,直线方程为7x﹣y+5=0,
故还存在一条公切线,其方程为7x﹣y+5=0.

练习册系列答案
相关题目
【题目】某校高一2班学生每周用于数学学习的时间![]() (单位:
(单位:![]() )与数学成绩
)与数学成绩![]() (单位:分)之间有如下数据:
(单位:分)之间有如下数据:
| 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.