题目内容
5.已知中心在坐标原点,焦点在x轴上的椭圆C的离心率为$\frac{1}{2}$,其一个顶点时抛物线x2=-4$\sqrt{3}$y的焦点.求椭圆C的标准方程.分析 由抛物线x2=-4$\sqrt{3}$y,可得焦点F.由题意可设椭圆C的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).根据题意可得$\frac{c}{a}$=$\frac{1}{2}$,b=$\sqrt{3}$,又a2=b2+c2.联立解出即可.
解答 解:由抛物线x2=-4$\sqrt{3}$y,可得焦点F$(0,-\sqrt{3})$.
由题意可设椭圆C的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
∵椭圆C的离心率为$\frac{1}{2}$,其一个顶点时抛物线x2=-4$\sqrt{3}$y的焦点.
∴$\frac{c}{a}$=$\frac{1}{2}$,b=$\sqrt{3}$,又a2=b2+c2.
解得c=1,a=2,
∴椭圆C的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
点评 本题考查了椭圆与抛物线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.直线l交椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1与M,N两点,椭圆的上顶点为B点,若△BMN的重心坐标为($\frac{1}{3}$,$\frac{1}{3}$),则直线l的方程是( )
| A. | 2x-4y+3=0 | B. | 2x-4y-3=0 | C. | 4x-2y-3=0 | D. | x-y-5=0 |
14.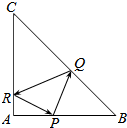 在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
 在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )| A. | $\frac{4}{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 4$\sqrt{2}$-4 |
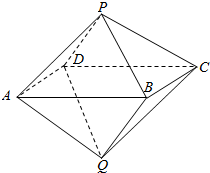 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1、2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1、2,AB=4.