题目内容
已知函数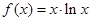 .
.
(1)求函数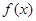 的极值点与极值;
的极值点与极值;
(2)设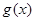 为
为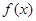 的导函数,若对于任意
的导函数,若对于任意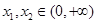 ,且
,且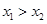 ,
,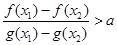 恒成立,求实数
恒成立,求实数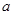 的取值范围.
的取值范围.
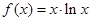 .
.(1)求函数
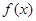 的极值点与极值;
的极值点与极值;(2)设
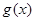 为
为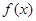 的导函数,若对于任意
的导函数,若对于任意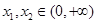 ,且
,且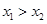 ,
,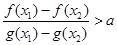 恒成立,求实数
恒成立,求实数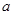 的取值范围.
的取值范围.(1)极小值点为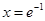 ,无极大值点;极小值为
,无极大值点;极小值为 ,无极大值. (2)
,无极大值. (2) .
.
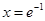 ,无极大值点;极小值为
,无极大值点;极小值为 ,无极大值. (2)
,无极大值. (2) .
.试题分析:(1)
 ,若
,若 ,则
,则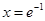 ,
, |  |  |  |
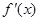 | 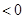 |  |  |
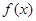 | 递增 |  | 递减 |
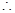 极小值点为
极小值点为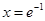 ,无极大值点;极小值为
,无极大值点;极小值为 ,无极大值. 6分
,无极大值. 6分(2)
 ,
, 对于任意
对于任意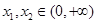 ,且
,且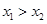 ,
,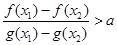 恒成立,
恒成立,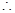 对于任意
对于任意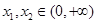 ,且
,且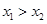 ,
,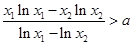 恒成立,
恒成立, 在
在 上单调递增,
上单调递增, ,
,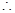 对于任意
对于任意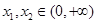 ,且
,且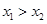 ,
, 恒成立,
恒成立,即
 恒成立, 9分
恒成立, 9分令
 ,
,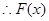 在
在 上单调递增,
上单调递增,  在
在 上恒成立, 11分
上恒成立, 11分法1.
 在
在 上恒成立,即
上恒成立,即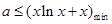 ,
,令
 ,
, ,
, 在
在 上递减,
上递减, 上递增,
上递增, ,
, . 15分
. 15分法2.令
 ,
, ,
,①当
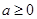 时,
时, 在
在 上单调递增,
上单调递增, 在
在 上不恒大于零,
上不恒大于零,如
 ,不符合,舍去;
,不符合,舍去;②当
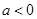 时,
时, 在
在 上递减,在
上递减,在 上递增,
上递增, ,
, .
.综上:
 . 15分
. 15分点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点.

练习册系列答案
相关题目
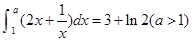 ,则
,则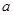 的值是 ;
的值是 ; 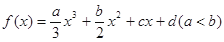 在
在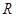 上单调递增,则
上单调递增,则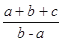 的最小值为( )
的最小值为( )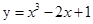 在点(1,f(x))处的切线方程为
在点(1,f(x))处的切线方程为 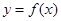 有三个零点
有三个零点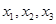 ,且在点
,且在点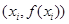 处的切线的斜率为
处的切线的斜率为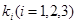 .则
.则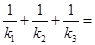 .
.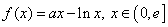 ,其中
,其中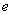 是自然常数,
是自然常数,
 时,
时, 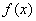 的单调性、极值;
的单调性、极值; ,使
,使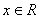 ,不等式
,不等式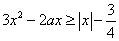 恒成立,则实数
恒成立,则实数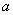 的范围 .
的范围 .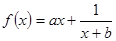 (
(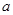 ,b∈Z),曲线
,b∈Z),曲线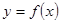 在点(2,
在点(2,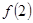 )处的切线方程为
)处的切线方程为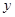 =3.
=3.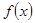 的解析式;
的解析式;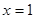 和直线
和直线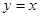 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.