题目内容
已知函数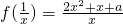 ,其中x∈(0,1]
,其中x∈(0,1]
(Ⅰ)当a= 时,求f(x)的最小值;
时,求f(x)的最小值;
(Ⅱ)在定义域内,f(x)>0恒成立,试求实数a的取值范围.
解:由题意知
∵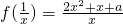 ,x∈(0,1]
,x∈(0,1]
设t= ∈[1,+∞),可求得函数f(x)的解析式为f(x)=
∈[1,+∞),可求得函数f(x)的解析式为f(x)=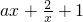 定义域为x∈[1,+∞)
定义域为x∈[1,+∞)
(Ⅰ)当a= 时,f(x)=
时,f(x)=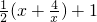 x∈[1,+∞)
x∈[1,+∞)
用定义证明f(x)的单调性如下:
设1≤x1<x2≤2,则f(x1)-f(x2)=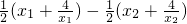 =
=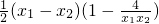 ,
,
∵1≤x1<x2≤2
∴f(x1)-f(x2 )>0
故f(x)在[1,2]上单调递减.同理可证f(x)在[2,+∞)上单调递增.
∴f(x)的最小值为f(2)=3.
(Ⅱ)∵x∈[1,+∞),f(x)=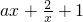 =
=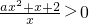 恒成立
恒成立
∴等价于当x∈[1,+∞),ax2+x+2>0恒成立即可
∴a>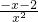 在x∈[1,+∞)恒成立 又
在x∈[1,+∞)恒成立 又 ∈(0,1]
∈(0,1]
令g(x)=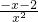 =-2(
=-2( )2-
)2- =-2(
=-2( +
+ )2+
)2+
即g(x)∈[-3,0)
∴a≥0
故a的取值范围[0,+∞).
分析:先利用换元法求其函数的解析式f(x)=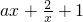 ,定义域为x∈[1,+∞),
,定义域为x∈[1,+∞),
(Ⅰ)把a的值代入解析式中,化简成“对号”函数的形式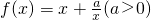 ,可以直接利用结论:
,可以直接利用结论:
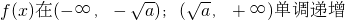 ,在
,在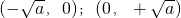 单调递减,可以求出最小值,也可以用定义证明函数的单调性,然后求其最值即可.
单调递减,可以求出最小值,也可以用定义证明函数的单调性,然后求其最值即可.
(Ⅱ)先化简不等式,f(x)>0,再由分式不等式等价转化整式不等式ax2+x+2>0恒成立,然后采用分离常数法求实数a的取值范围即可.
点评:本题对学生的程度要求比较高,有一定的难度,主要考查利用函数单调性求函数的最值,及不等式的等价转化思想.
∵
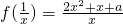 ,x∈(0,1]
,x∈(0,1]设t=
 ∈[1,+∞),可求得函数f(x)的解析式为f(x)=
∈[1,+∞),可求得函数f(x)的解析式为f(x)=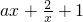 定义域为x∈[1,+∞)
定义域为x∈[1,+∞) (Ⅰ)当a=
 时,f(x)=
时,f(x)=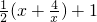 x∈[1,+∞)
x∈[1,+∞) 用定义证明f(x)的单调性如下:
设1≤x1<x2≤2,则f(x1)-f(x2)=
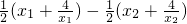 =
=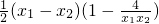 ,
,∵1≤x1<x2≤2
∴f(x1)-f(x2 )>0
故f(x)在[1,2]上单调递减.同理可证f(x)在[2,+∞)上单调递增.
∴f(x)的最小值为f(2)=3.
(Ⅱ)∵x∈[1,+∞),f(x)=
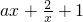 =
=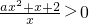 恒成立
恒成立∴等价于当x∈[1,+∞),ax2+x+2>0恒成立即可
∴a>
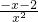 在x∈[1,+∞)恒成立 又
在x∈[1,+∞)恒成立 又 ∈(0,1]
∈(0,1]令g(x)=
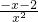 =-2(
=-2( )2-
)2- =-2(
=-2( +
+ )2+
)2+
即g(x)∈[-3,0)
∴a≥0
故a的取值范围[0,+∞).
分析:先利用换元法求其函数的解析式f(x)=
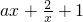 ,定义域为x∈[1,+∞),
,定义域为x∈[1,+∞),(Ⅰ)把a的值代入解析式中,化简成“对号”函数的形式
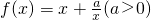 ,可以直接利用结论:
,可以直接利用结论: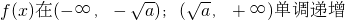 ,在
,在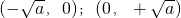 单调递减,可以求出最小值,也可以用定义证明函数的单调性,然后求其最值即可.
单调递减,可以求出最小值,也可以用定义证明函数的单调性,然后求其最值即可.(Ⅱ)先化简不等式,f(x)>0,再由分式不等式等价转化整式不等式ax2+x+2>0恒成立,然后采用分离常数法求实数a的取值范围即可.
点评:本题对学生的程度要求比较高,有一定的难度,主要考查利用函数单调性求函数的最值,及不等式的等价转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.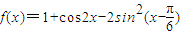 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移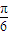 得到函数f(x)的图象
得到函数f(x)的图象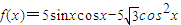 (其中x∈R).
(其中x∈R).