Question

（2004•宁波模拟）已知一个棱锥被平行于底面的两个平面截为三部分，最上面的部分是一个小棱锥，其余两部分都是棱台，若这三部分的高相等，则上、中、下三部分的体积之比为

1：7：19

．

Answer 1

分析：由已知中从顶点起将锥体（圆锥或棱锥）的高三等分，过两个分点分别作平行于底面的截面，两个截面将锥体的体积依次分成三部分，体积分别为V₁，V₂，V₃，我们根据相似的性质，求出三个相应锥体的体积之比，相减后即可得到答案．

解答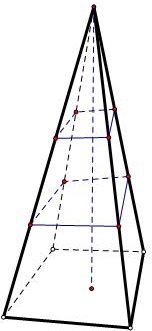：解：由已知中从顶点起将锥体（圆锥或棱锥）的高三等分，过两个分点分别作平行于底面的截面，
则以分别以原来底面和两个截面为底面的锥体，是相似几何体
相似比为1：2：3
根据相似的性质三个锥体的相似比为：1³：2³：3³=1：8：27
则上、中、下三部分的体积之比V₁：V₂：V₃=1：（8-1）：（27-8）=1：7：19
故答案为：1：7：19．

点评：本题考查棱锥的结构特征，考查棱锥的性质，棱锥的体积等．解答关键在于相似多边形面积之比等于相似比的平方，其中利用相似的性质，线之比等于相似比，面积之比等于相似比的平方，体积之比等于相似比的立方．