Question

【题目】若无穷数列满足：存在，对任意的，都有（为常数），则称具有性质

（1）若无穷数列具有性质，且，求的值

（2）若无穷数列是等差数列，无穷数列是公比为正数的等比数列，，，，判断是否具有性质，并说明理由.

（3）设无穷数列既具有性质，又具有性质，其中互质，求证：数列具有性质

Answer 1

【答案】（1）6；（2）不具有；详见解析（3）证明见解析；

【解析】

（1）由题意可得任意的，都有，可得，即可得解；

（2）由题意可得，若具有性质，由新定义可得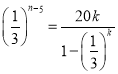，即可判断；

（3）由题意可得对任意，均有，，进而可得、、，再证明即可得解.

（1）无穷数列具有性质，

，，

又，即，

；

（2）设无穷数列的公差为d，无穷数列公比为q，，

则，，，，

，，，

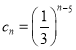假设具有性质，，

则对于任意的，

均有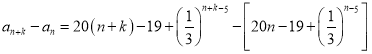

，

即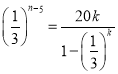对任意均成立，式子左边是变量，右边是常数，所以

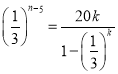不恒成立，故假设错误，

不具有性质；

（3）证明：无穷数列具有性质，

，，①

无穷数列具有性质，

，，②

互质，

由①得，由②得，

即，

当时，，

数列具有性质.