Question

(本小题满分12分)

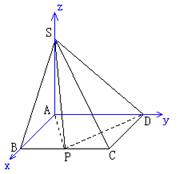
如图,四棱锥S-ABCD的底面是矩形,AB=a，AD=2，SA=1，且SA⊥底面ABCD，若边BC上存在异于B，C的一点P，使得.

（1）求a的最大值；

（2）当a取最大值时，求异面直线AP与SD所成角的余弦值．

 

Answer 1

【答案】

 

解：建立如图所示的空间直角坐标系,则各点坐标分别为:

   A(0, 0,0),B(a,0,0),C(a,2,0),D(0,2,0),S(0,0,1),设P(a,x,0)，(0<x<2)

   (1) ∵………3分

∴由得: ×=0,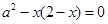

即: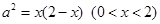

∴当且仅当x=1时,a有最大值为1.

此时P为BC中点；                ………6分

(2) 由(1)知:                        ………8分

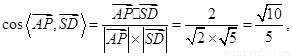∴             ………10分

∴异面直线AP与SD所成角的余弦值为．                 ………12分

 

【解析】略