题目内容
P为双曲线
上的一点，F为一个焦点，以PF为直径的圆与圆
的位置关系是（ ）
A．内切
B．内切或外切
C．外切
D．相离或相交
【答案】
B
【解析】主要考查双曲线定义、标准方程及圆与圆的位置关系。
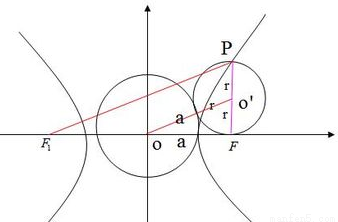
解：如图所示，由双曲线定义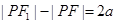
，即
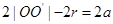，所以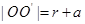
，以PF为直径的圆与圆
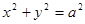的位置关系是外切；同理，若P在左支上，以PF为直径的圆与圆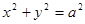的位置关系是内切，故选B。
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
已知F1、F2分别是双曲线
-
=1（a＞0，b＞0）的左、右焦点，P为双曲线上的一点，若∠F1PF2=90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | B、3 | C、4 | D、5 |
已知F1、F2分别是双曲线
-
=1(b＞0)的左、右焦点，P为双曲线上的一点，若∠F1PF2=120°，且△F1PF2的三边长成等差数列，则双曲线的渐近线的斜率是（ ）
| x2 |
| 4 |
| y2 |
| b2 |
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
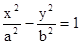（a>0,b>0）的左、右焦点，P为双曲线上的一点，若
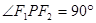,且
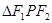的三边长成等差数列，则双曲线的离心率是（
）