题目内容
如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
(1)求证:DC是⊙O的切线;
(2)若EB=6,EC=6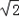 ,求BC的长.
,求BC的长.
(1)求证:DC是⊙O的切线;
(2)若EB=6,EC=6
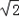 ,求BC的长.
,求BC的长.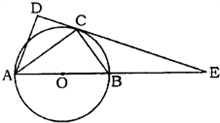
(1)证明:∵⊙O是以AB为直径的圆,∠ACB=90°,
∴点C在⊙O上,连接OC,可得∠OCA=∠OAC=∠DAC,
∴OC∥AD,
又∵AD⊥DC,
∴DC⊥OC,
∵OC为半径,
∴DC是⊙O的切线.
(2)解:∵DC是⊙O的切线,
∴EC2=EB·EA,
又∵EB=6,EC=6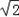 ,
,
∴EA=12.
∵∠ECB=∠EAC,∠CEB=∠AEC,
∴△ECB∽△EAC,
∴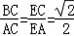 ,AC=
,AC=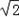 BC,
BC,
∵AC2+BC2=AB2=36,
∴BC=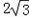

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
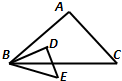 如图,在△ABC和△DBE中,
如图,在△ABC和△DBE中,| AB |
| DB |
| BC |
| BE |
| AC |
| DE |
| 5 |
| 3 |
| A、20cm | ||
B、
| ||
C、
| ||
| D、25cm |
 (2011•徐州模拟)如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若
(2011•徐州模拟)如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若 如图,在△ABC和△AEF中,B是EF的中点,AB=EF=2,CA=CB=3,若
如图,在△ABC和△AEF中,B是EF的中点,AB=EF=2,CA=CB=3,若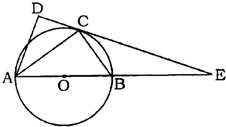 (2012•商丘二模)选修4-1:几何证明选讲
(2012•商丘二模)选修4-1:几何证明选讲 ,若
,若 ,则
,则 与
与 的夹角等于 .
的夹角等于 .