题目内容

如图，在△ABC和△AEF中，B是EF的中点，AB=EF=2，CA=CB=3，若
AB
•
AE
+
AC
•
AF
=7，则
EF
与
BC
的夹角的余弦值等于
1
3
1
3
．
分析：由题意可得
BC
2=9=(
AC
- 
AB
)2，由此求得
AC
•
AB
=2，由
AB
•
AE
+
AC
•
AF
=7以及两个向量的加减法的法则及其几何意义可求得
EF
•
BC
=2，即2×3×cos＜
EF
，
BC
＞=2，由此求得
EF
与
BC
的夹角的余弦值．
解答：解：由题意可得
BC
2=9=(
AC
- 
AB
)2=
AC
2+
AB
2-2
AC
•
AB
=9+4-2
AC
•
AB
，∴
AC
•
AB
=2．
由
AB
•
AE
+
AC
•
AF
=7，可得
AB
•(
AB
+
BE
)+
AC
•(
AB
+
BF
)=
AB
2+
AB
•
BE
+
AC
•
AB
+
AC
•
BF
=4+
AB
•(-
BF
)+2+
AC
•
BF

=6+
BF
•(
AC
-
AB
)=6+
1
2
EF
•
BC
，
∴
EF
•
BC
=2，即 2×3×cos＜
EF
，
BC
＞=2，
∴cos＜
EF
，
BC
＞=
1
3
，
故答案为
1
3
．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义、以及运算性质，属于中档题．
练习册系列答案
相关题目
（2011•徐州模拟）如图，在△ABC和△AEF中，B是EF的中点，AB=EF=1，CA=CB=2，若
AB
•
AE
+
AC
•
AF
=2，则
EF
与
BC
的夹角等于
π
3
π
3
．
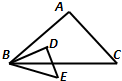精英家教网如图，在△ABC和△DBE中，
AB
DB
=
BC
BE
=
AC
DE
=
5
3
，若△ABC与△DBE的周长之差为10cm，则△ABC的周长为（　　）
A、20cm
B、
25
4
cm
C、
50
3
cm
D、25cm
（2012•商丘二模）选修4-1：几何证明选讲
如图，在△ABC和△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD，⊙O是以AB为直
径的圆，DC的延长线与AB的延长线交于点E．
（Ⅰ）求证：DC是⊙O的切线；
（Ⅱ）若EB=6，EC=6
2
，求BC的长．

如图，在△ABC和△AEF中，B是EF的中点，AB=EF=1，，若

，则与的夹角等于        ．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网