题目内容
已知函数f(x)=sinxcosx+
cos2x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间[-
,
]上的最大值和最小值.
| 3 |
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间[-
| π |
| 6 |
| π |
| 2 |
(Ⅰ)∵f(x)=sinxcosx+
cos2x=
•2sinxcosx+
(cos2x+1)
=
sin2x+
cos2x+
=sin(2x+
)+
,∴函数f(x)的最小正周期T=
=π.
(Ⅱ)∵-
≤x≤
,0≤2x+
≤
,∴-
≤sin(2x+
)≤1,
∴0≤sin(2x+
)+
≤1+
=
,∴f(x)在区间[-
,
]上的最大值为
,最小值为0.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
| 2π |
| 2 |
(Ⅱ)∵-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
| ||
| 2 |
| π |
| 3 |
∴0≤sin(2x+
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
2+
| ||
| 2 |
| π |
| 6 |
| π |
| 2 |
2+
| ||
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
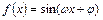 (
(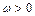 ,
,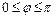 )为偶函数,且其图像上相邻的一个最高点和最低点之间距离为
)为偶函数,且其图像上相邻的一个最高点和最低点之间距离为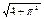 .
.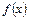 的解析式;
的解析式;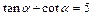 ,求
,求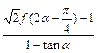 的值。
的值。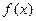 是定义在(0,3)上的函数,
是定义在(0,3)上的函数,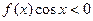 的解集是( )
的解集是( )
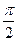 )∪(
)∪( ,则
,则




 = .
= . ,则
,则 .
.