题目内容
已知函数f(x)=sin(2x+
),下面结论错误的是( )
| 3π |
| 2 |
| A.函数f(x)的最小正周期为π | ||
| B.函数f(x)是偶函数 | ||
C.函数f(x)的图象关于直线x=
| ||
D.函数f(x)在区间[0,
|
对于函数f(x)=sin(2x+
)=-cos2x,它的周期等于
=π,故A正确.
由于f(-x)=-cos(-2x)=-cos2x=f(x),故函数f(x)是偶函数,故B正确.
令x=
,则f(
)=sin(2×
+
)=0,故f(x)的一个对称中心,故C错误.
由于0≤x≤
,则0≤2x≤π,
由于函数y=cost在[0,π]上单调递减
故y=-cost在[0,π]上单调递增,故D正确.
故选C.
| 3π |
| 2 |
| 2π |
| 2 |
由于f(-x)=-cos(-2x)=-cos2x=f(x),故函数f(x)是偶函数,故B正确.
令x=
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
由于0≤x≤
| π |
| 2 |
由于函数y=cost在[0,π]上单调递减
故y=-cost在[0,π]上单调递增,故D正确.
故选C.

练习册系列答案
相关题目
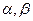 满足:
满足: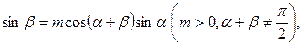 令
令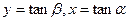
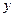 表示成
表示成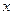 的不含
的不含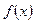 (即写出
(即写出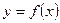 的解析式),
的解析式),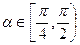 时,求函数
时,求函数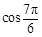 = .
= .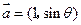 ,
,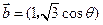 ,则
,则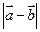 的最大值为 .
的最大值为 . ,
, ,
, ,则
,则 的值_________.
的值_________. 的值是_______.
的值是_______.