题目内容
已知椭圆C: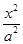 +
+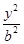 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为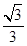 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为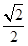 .
.
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有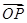 =
=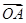 +
+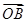 成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
【答案】
(Ⅰ)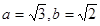 ;(Ⅱ)P(
;(Ⅱ)P(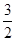 ,±
,±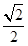 ),
),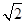 x±y-
x±y-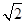 =0.
=0.
【解析】
试题分析:(Ⅰ) 先利用点到直线的距离公式求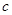 ,再利用离心率求
,再利用离心率求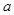 ,最后利用参数的关系求
,最后利用参数的关系求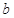 ;(Ⅱ)设点利用方程组消元后得根与系数关系,然后代入题中条件化简可求.
;(Ⅱ)设点利用方程组消元后得根与系数关系,然后代入题中条件化简可求.
试题解析:(Ⅰ) 设F(c,0),当l的斜率为1时,其方程为x-y-c=0,
∴O到l的距离为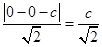 ,
,
由已知,得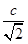 =
=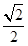 ,∴c=1.
,∴c=1.
由e=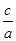 =
=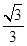 ,得a=
,得a=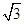 ,b=
,b=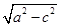 =
=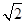 .
4分
.
4分
(Ⅱ)假设C上存在点P,使得当l绕F转到某一位置时,有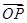 =
=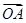 +
+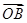 成立,
成立,
设A(x1,y1),B(x2,y2),则P(x1+x2,y1+y2).
由(Ⅰ),知C的方程为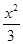 +
+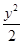 =1.
=1.
由题意知,l的斜率一定不为0,故不妨设l:x=ty+1.
由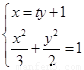 ,消去x并化简整理,得(2t2+3)y2+4ty-4=0.
,消去x并化简整理,得(2t2+3)y2+4ty-4=0.
由韦达定理,得y1+y2=-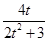 ,
,
∴x1+x2=ty1+1+ty2+1=t(y1+y2)+2=-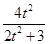 +2=
+2=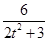 ,
,
∴P(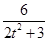 ,-
,-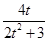 ).
).
∵点P在C上,∴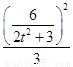 +
+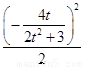 =1,
=1,
化简整理,得4t4+4t2-3=0,即(2t2+3)(2t2-1)=0,解得t2=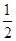 .
.
当t=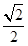 时,P(
时,P(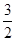 ,-
,-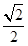 ),l的方程为
),l的方程为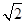 x-y-
x-y-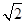 =0;
=0;
当t=-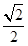 时,P(
时,P(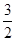 ,
,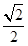 ),l的方程为
),l的方程为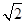 x+y-
x+y-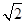 =0.
=0.
故C上存在点P(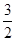 ,±
,±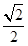 ),使
),使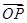 =
=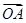 +
+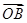 成立,此时l的方程为
成立,此时l的方程为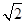 x±y-
x±y-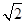 =0. 13分
=0. 13分
考点:椭圆的基本概念,点到直线的距离,根与系数关系,设而不求的思想.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为 .
. =
= +
+ 成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.