题目内容
(2013•福建)设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
分析:A项,x0(x0≠0)是f(x)的极大值点,不一定是最大值点,故不正确;
B项,f(-x)是把f(x)的图象关于y轴对称,因此,-x0是f(-x)的极大值点;
C项,-f(x)是把f(x)的图象关于x轴对称,因此,x0是-f(x)的极小值点;
D项,-f(-x)是把f(x)的图象分别关于x轴、y轴做对称,因此-x0是-f(-x)的极小值点.
B项,f(-x)是把f(x)的图象关于y轴对称,因此,-x0是f(-x)的极大值点;
C项,-f(x)是把f(x)的图象关于x轴对称,因此,x0是-f(x)的极小值点;
D项,-f(-x)是把f(x)的图象分别关于x轴、y轴做对称,因此-x0是-f(-x)的极小值点.
解答:解:对于A项,x0(x0≠0)是f(x)的极大值点,不一定是最大值点,因此不能满足在整个定义域上值最大;
对于B项,f(-x)是把f(x)的图象关于y轴对称,因此,-x0是f(-x)的极大值点;
对于C项,-f(x)是把f(x)的图象关于x轴对称,因此,x0是-f(x)的极小值点;
对于D项,-f(-x)是把f(x)的图象分别关于x轴、y轴做对称,因此-x0是-f(-x)的极小值点.
故选D.
对于B项,f(-x)是把f(x)的图象关于y轴对称,因此,-x0是f(-x)的极大值点;
对于C项,-f(x)是把f(x)的图象关于x轴对称,因此,x0是-f(x)的极小值点;
对于D项,-f(-x)是把f(x)的图象分别关于x轴、y轴做对称,因此-x0是-f(-x)的极小值点.
故选D.
点评:本题考查函数的极值,考查函数图象的对称性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
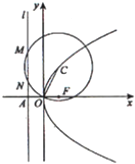 (2013•福建)如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
(2013•福建)如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.