题目内容
(本小题满分12分)三次函数 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为 ,
, ,
, ,
, 求证
求证  ;
;

【答案】
解:(1)由已知得a=c=0,b=-4,当x<0时
当且仅当x=-2时取得最大值-4 3分
3分
(2)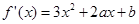 ,依题意有
,依题意有 ……5分
……5分
从而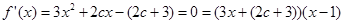 ,令
,令
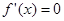 有
有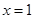 或
或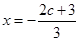 由于
由于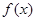 在
在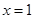 处取得极值,因此
处取得极值,因此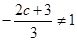 ,得到
,得到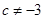
1若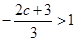 ,即
,即 ,则当
,则当 时,
时, ,因此
,因此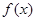 的单调递减区间为
的单调递减区间为 ;
………………………………7分
;
………………………………7分
2若 ,即
,即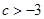 ,则当
,则当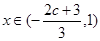 时,
时, ,因此
,因此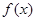 的单调递减区间为
的单调递减区间为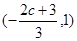 。…………………………………………8分
。…………………………………………8分
(3)设直线BD的方程为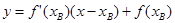 因为D点在直线上又在曲线上,所以
因为D点在直线上又在曲线上,所以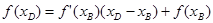 即
即

得到: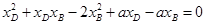 从而
从而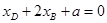 ,同理有
,同理有
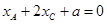 ,由于AC平行于BD,因此
,由于AC平行于BD,因此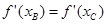 ,
,
得到
进一步化简可以得到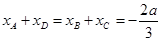 ,从而
,从而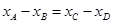
又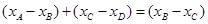 ,
,
因此 ………………………12分
………………………12分
【解析】略

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目