题目内容
函数f(x)= cosx- cos(x+ )的最大值为 ( )
)的最大值为 ( )
| A.2 | B. | C.1 | D. |
C
解析试题分析:利用两角和差的正弦、余弦公式化简函数的解析式为f(x)=sin(x+ ),再由正弦函数的有界性求得它的最大值..根据题意可知故函数f(x)= f(x)= cosx- cos(x+
),再由正弦函数的有界性求得它的最大值..根据题意可知故函数f(x)= f(x)= cosx- cos(x+ )化简变形为f(x)=sin sin(x+
)化简变形为f(x)=sin sin(x+ ),那么借助于正弦函数的性质可知其最大值为1,故选C
),那么借助于正弦函数的性质可知其最大值为1,故选C
考点:两角和差的正弦、余弦公式
点评:本题主要考查两角和差的正弦、余弦公式的应用,正弦函数的有界性,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知sin ,则sin
,则sin
A. | B.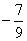 | C. | D. |
 的值是( )
的值是( )
A.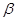 | B. | C. | D. |
为了得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平移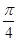 个长度单位 个长度单位 | B.向右平移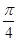 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
函数 一个周期内的图象如图,其中
一个周期内的图象如图,其中 ,且
,且 两点在
两点在 轴两侧,则下列区间是
轴两侧,则下列区间是 的单调区间的是 ( )
的单调区间的是 ( )
A. | B. | C. | D. |
有以下四种变换方式:
向左平行移动 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的 ;
;
向右平行移动 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的 ;
;
每个点的横坐标缩短为原来的 ,再向右平行移动
,再向右平行移动 个单位长度;
个单位长度;
每个点的横坐标缩短为原来的 ,再向左平行移动
,再向左平行移动 个单位长度.
个单位长度.
其中能将函数 的图象变为函数
的图象变为函数 的图象的是( )
的图象的是( )
| A.①和④ | B.①和③ | C.②和④ | D.②和③ |
 = ( )
= ( )
A. | B. | C. | D. |
设 角属于第二象限,且
角属于第二象限,且 ,则
,则 角属于( )
角属于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
函数y=2tan(3x- )的一个对称中心是 ( )
)的一个对称中心是 ( )
A.( ,0) ,0) | B.( ,0) ,0) | C.( ,0) ,0) | D.(- ,0) ,0) |