题目内容
4.已知中心在原点的椭圆C的一个焦点为F(0,1),离心率为$\frac{1}{2}$,则椭圆C的标准方程为$\frac{y^2}{4}+\frac{x^2}{3}=1$.分析 由题意可知,椭圆是焦点在y轴上的椭圆,再由已知得到c=1,结合离心率求出a,根据隐含条件求得b,则椭圆方程可求.
解答 解:由题意可知,椭圆的标准方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1(a>b>0)$,
又椭圆C的一个焦点为F(0,1),离心率为$\frac{1}{2}$,
可得c=1,a=2,∴b2=a2-c2=4-1=3.
∴椭圆C的标准方程为$\frac{y^2}{4}+\frac{x^2}{3}=1$.
故答案为:$\frac{y^2}{4}+\frac{x^2}{3}=1$.
点评 本题考查椭圆的简单性质,考查了椭圆标准方程的求法,是基础题.

练习册系列答案
相关题目
15.P(x,y)在线段AB上运动,已知A(2,4),B(5,-2),则$\frac{y+1}{x+1}$的取值范围是( )
| A. | [-$\frac{1}{6}$,$\frac{5}{3}$] | B. | (-∞,-$\frac{1}{6}$]∪[$\frac{5}{3}$,+∞) | C. | [-$\frac{1}{6}$,0)∁(0,$\frac{5}{3}$] | D. | (-$\frac{1}{6}$,$\frac{5}{3}$) |
12.若椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1的离心率为$\frac{1}{2}$,则m=( )
| A. | $\frac{9}{4}$ | B. | 4 | C. | $\frac{9}{4}$或4 | D. | $\frac{3}{2}$ |
19.下列有关命题的说法中错误的是( )
| A. | “若x2+y2=0,则x,y全为0”的否命题是真命题 | |
| B. | 函数f(x)=ex+x-2的零点所在区间是(1,2) | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1则x2-3x+2≠0” | |
| D. | 对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0 |
16.下面是一程序,该程序的运行结果是( )


| A. | 1,2 | B. | 1,1 | C. | 2,1 | D. | 2,2 |
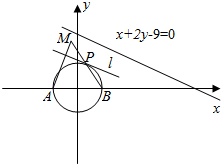 已知圆C:x2+y2=1与x轴的两个交点分别为A,B(由左到右),P为C上的动点,l过点P且与C相切,过点A作l的垂线且与直线BP交于点M,则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$.
已知圆C:x2+y2=1与x轴的两个交点分别为A,B(由左到右),P为C上的动点,l过点P且与C相切,过点A作l的垂线且与直线BP交于点M,则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$.