题目内容
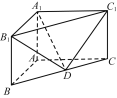
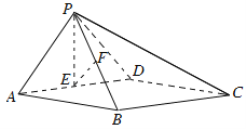
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
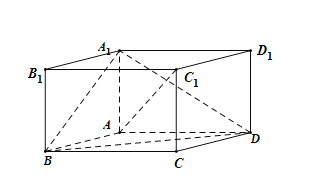
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】试题分析:(1)先根据条件建立空间直角坐标系,进而得相关点的坐标,求出直线A1B与AC1的方向向量,根据向量数量积求出方向向量夹角,最后根据异面直线所成角与方向向量夹角之间相等或互补可得夹角的余弦值;(2)根据建立的空间直角坐标系,得相关点的坐标,求出各半平面的法向量,根据向量数量积求出法向量的夹角,最后根据二面角与法向量夹角之间关系确定二面角的正弦值.
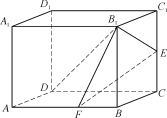
试题解析:解:在平面ABCD内,过点A作AE![]() AD,交BC于点E.
AD,交BC于点E.
因为AA1![]() 平面ABCD,
平面ABCD,
所以AA1![]() AE,AA1
AE,AA1![]() AD.
AD.
如图,以![]() 为正交基底,建立空间直角坐标系A-xyz.
为正交基底,建立空间直角坐标系A-xyz.
因为AB=AD=2,AA1=![]() ,
, ![]() .
.
则![]() .
.
(1) ![]() ,
,
则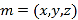 .
.
因此异面直线A1B与AC1所成角的余弦值为![]() .
.
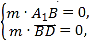
(2)平面A1DA的一个法向量为![]() .
.
设![]() 为平面BA1D的一个法向量,
为平面BA1D的一个法向量,
又![]() ,
,
则![]() 即
即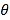
不妨取x=3,则![]() ,
,
所以![]() 为平面BA1D的一个法向量,
为平面BA1D的一个法向量,
从而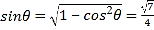 ,
,
设二面角B-A1D-A的大小为![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
因此二面角B-A1D-A的正弦值为![]() .
.
点睛:利用法向量求解空间线面角、面面角的关键在于“四破”:①破“建系关”,构建恰当的空间直角坐标系;②破“求坐标关”,准确求解相关点的坐标;③破“求法向量关”,求出平面的法向量;④破“应用公式关”.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: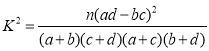 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |