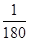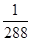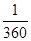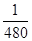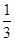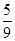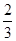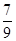题目内容
(1)甲盒中有红,黑,白三种颜色的球各3个,乙盒子中有黄,黑,白三种颜色的球各2个,从两个盒子中各取1个球,求取出的两个球是不同颜色的概率。
(2)在单位圆的圆周上随机取三点A、B、C,求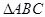 是锐角三角形的概率。
是锐角三角形的概率。
(2)在单位圆的圆周上随机取三点A、B、C,求
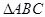 是锐角三角形的概率。
是锐角三角形的概率。(1)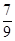 (2)
(2)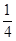
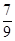 (2)
(2)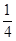
试题分析:(1) 解:(1)设A=“取出的两球是相同颜色”,B=“取出的两球是不同颜色”,则事件A的概率为: P(A)=
 =
=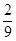 。 由于事件A与事件B是对立事件,所以事件B的概率为:
。 由于事件A与事件B是对立事件,所以事件B的概率为:P(B)=1-P(A)=1-
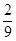 =
=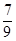
(2)记
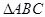 的三内角分别为
的三内角分别为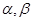 ,
,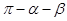 ,事件A表示“
,事件A表示“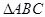 是锐角三角形”,则试验的全部结果组成集合
是锐角三角形”,则试验的全部结果组成集合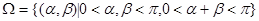 。
。因为
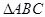 是锐角三角形的条件是
是锐角三角形的条件是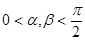 且
且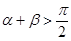
所以事件A构成集合
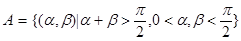
所求概率为
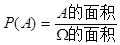
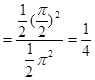 。
。点评:古典概型概率首先找到所有基本事件总数与满足题意要求的基本事件种数,求其比值即可;几何概型概率通常找长度比,面积比或体积比

练习册系列答案
相关题目
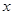 表示第
表示第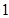 枚骰子出现的点数,
枚骰子出现的点数,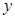 表示第
表示第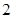 枚骰子出现的点数.
枚骰子出现的点数. 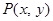 在直线
在直线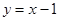 上的概率;
上的概率; 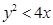 的概率.
的概率.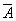 是A的对立事件,
是A的对立事件,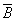 是B的对立事件。若和事件A+B发生的概率为0.4,则积事件
是B的对立事件。若和事件A+B发生的概率为0.4,则积事件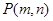 落在圆x2+y2=16内的概率是.
落在圆x2+y2=16内的概率是.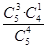
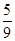 )3×
)3×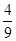
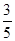 ×
×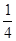
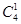 ×(
×(