题目内容
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=-
(Ⅰ)求当x<0时,f(x)的解析式;
(Ⅱ)试确定函数y=f(x)(x≥0)的单调区间,并证明你的结论;
(Ⅲ)(理)若x1≥2,且x2≥2
证明:|f(x1)-f(x2)|<2.
答案:
解析:
解析:
|
解:(Ⅰ)若x<0则-x>0, ∵f(x)是偶函数, ∴f(x)=f(-x)=- (Ⅱ)设x1,x2是区间[0,+∞)上的任意两个实数,且0≤x1<x2, 则f(x1)-f(x2)= 当0≤x1<x2≤1时,x1-x2<0,x1x2-1<0 而x12+x1+1>0及x22+x2+1>0 ∴f(x1)-f(x2)>0即f(x)在[0,1]上为减函数 同理,当1<x1<x2时,f(x1)-f(x2)<0, 即f(x)在(1,+∞)上为增函数 (Ⅲ)(理)∵f(x)在(1,+∞)是增函数, 由x≥2得f(x)≥f(2)=-2 又x2+x+1>0,-7x<0 ∴f(x)=- ∴-2≤f(x)<0 ∵x1,x2≥2 ∴-2≤f(x1)<0且-2≤f(x2)<0即0<-f(x2)≤2 ∴-2<f(x1)-f(x2)<2 ∴|f(x1)-f(x2)|<2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
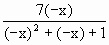 =
=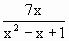 (x<0)
(x<0)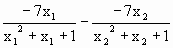 =
=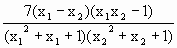
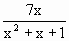 <0,
<0,