题目内容
(2007•温州一模)设a>0且a≠1,若函数f(x)=
在x=0处连续,则
f(x)=
|
| lim |
| x→a- |
2
2
.分析:根据题意可得 loga(a+0)=
,解得 a=2,故要求的式子为
=
,由此
求出它的极限.
| 4-0 |
| 2(a-0) |
| lim |
| x→2- |
| 4-x2 |
| 2(2-x) |
| lim |
| x→2- |
| 2+x |
| 2 |
求出它的极限.
解答:解:∵a>0且a≠1,若函数f(x)=
在x=0处连续,
∴loga(a+0)=
,∴a=2.
∴
f(x)=
=
=
=2,
故答案为:2.
|
∴loga(a+0)=
| 4-0 |
| 2(a-0) |
∴
| lim |
| x→a- |
| lim |
| x→2- |
| 4-x2 |
| 2(2-x) |
| lim |
| x→2- |
| (2-x)(2+x) |
| 2(2-x) |
| lim |
| x→2- |
| 2+x |
| 2 |
故答案为:2.
点评:本题主要考查分段函数的应用,函数在某处连续的定义,求函数的极限的方法,求出a=2是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
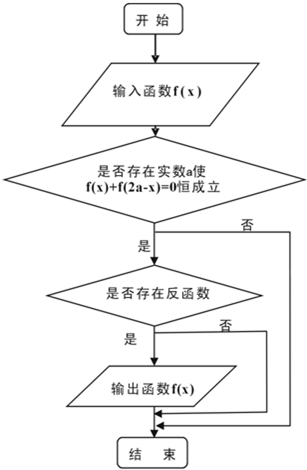 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )