题目内容
用“五点法”画出函数y=
sinx+2,x∈[0,2π]的简图(要求必须列表、描点、再连线)并在图形上找出当x取何值时,函数有最值,最值是多少?
| 1 | 2 |
分析:根据正弦函数的图象与性质,利用“五点法”作图的一般步骤,先列表、再描点,最后连成平滑的曲线,可得函数y=
sinx+2在[0,2π]上的简图,如图所示.由作出的图象,不难得到函数的最大、最小值相应的x值.
| 1 |
| 2 |
解答:解:先列表

可得五个点的坐标为A(0,2),B(
,
),C(π,2),D(
,
),E(2π,2)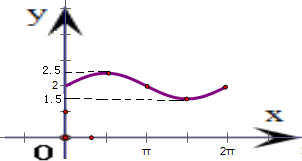
将这五个点连成平滑的曲线,得到函数的图象如图所示
由图象可得
当x=
时,函数有最大值等于
;
当x=
时,函数有最小值等于
.

可得五个点的坐标为A(0,2),B(
| π |
| 2 |
| 5 |
| 2 |
| 3π |
| 2 |
| 3 |
| 2 |

将这五个点连成平滑的曲线,得到函数的图象如图所示
由图象可得
当x=
| π |
| 2 |
| 5 |
| 2 |
当x=
| 3π |
| 2 |
| 3 |
| 2 |
点评:本题利用“五点法”作三角函数的图象,并求函数的最值.着重考查了三角函数的图象与性质、正弦函数的最值及相应的x值等知识,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 已知函数
已知函数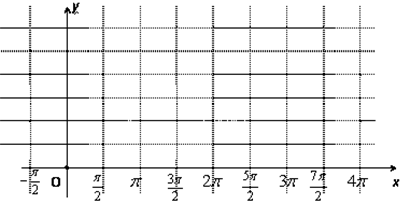
 已知函数
已知函数 .
.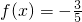 ,
, ,求sin2x的值.
,求sin2x的值.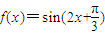 .
.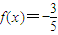 ,
,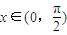 ,求sin2x的值.
,求sin2x的值.