题目内容
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求恰好第2次中奖的概率;
(Ⅱ)从中有放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).
(1)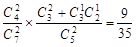 (2)
(2)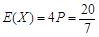
解析试题分析:解(Ⅰ)“恰好第2次中奖”即为“第一次摸到的2个白球,第二次至少有1个红球”,其概率为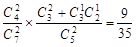 .
.
(Ⅱ)摸一次中奖的概率为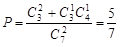 .
.
由条件知X~B(4, P),∴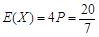 .
.
考点:二项分布
点评:解决的关键是根据排列组合的知识表示概率值,然后借助于独立重复试验来得到,属于基础题。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| | “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为
 ,其中
,其中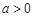 ,
,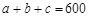 。当数据
。当数据 的方差
的方差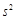 最大时,写出
最大时,写出 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时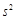 的值.
的值.(注:
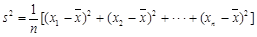 ,其中
,其中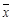 为数据
为数据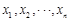 的平均数)
的平均数) 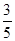 ,乙队获胜的概率为
,乙队获胜的概率为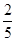 ,且每局比赛的胜负是相互独立的,问:
,且每局比赛的胜负是相互独立的,问: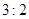 获胜的概率是多少?
获胜的概率是多少? 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
. ;
; 为落入
为落入 的概率和
的概率和 .
.

 区域返券60元;停在
区域返券60元;停在 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
 (元),求随机变量
(元),求随机变量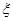 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求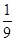 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为 ,试写出
,试写出