题目内容
 在等边三角形ABC中,AB=a,O为△ABC的中心,过O的直线交AB于M,交AC于N,求
在等边三角形ABC中,AB=a,O为△ABC的中心,过O的直线交AB于M,交AC于N,求| 1 |
| OM2 |
| 1 |
| ON2 |
分析:如图所示,建立直角坐标系.可得A(0,
a),B(-
a,0),C(
a,0),O(0,
).可得直线AB、AC的方程,设直线MN的斜率为k,则y=kx+
a.分别与直线AB、AC方程联立可得点M,N的坐标,再利用两点间的距离公式可得
+
关于k,a的表达式,利用斜率k的取值范围和反比例函数的单调性即可得出最大值和最小值
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 6 |
| 1 |
| OM2 |
| 1 |
| ON2 |
解答:解:如图所示,建立直角坐标系.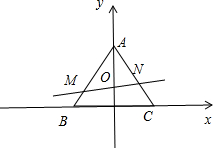
则A(0,
a),B(-
a,0),C(
a,0),O(0,
).
可得直线AB、AC的方程分别为
+
=1,
+
=1,
分别化为-x+
=
a,x+
=
a.
设直线MN的斜率为k,则y=kx+
a.(-
≤k≤
).
联立
与
,
解得M(
,
),N(
,
).
∴|OM|2=(
)2+[
-
]2=
,
|ON|2=(
)2+[
-
]2=
.
∴
+
=
=
=
(1+
),
∵-
≤k≤
,∴0≤k2≤
,∴
≤
≤2.
∴
≤
(1+
)≤
.
∴
+
的最大值和最小值分别为
,
.
从图形上看:当MN∥BC时取得最小值,当MN与AC边上的中线重合时取得最大值.

则A(0,
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 6 |
可得直线AB、AC的方程分别为
| x | ||
-
|
| y | ||||
|
| x | ||
|
| y | ||||
|
分别化为-x+
| y | ||
|
| 1 |
| 2 |
| y | ||
|
| 1 |
| 2 |
设直线MN的斜率为k,则y=kx+
| ||
| 6 |
| ||
| 3 |
| ||
| 3 |
联立
|
|
解得M(
| a | ||
|
a(
| ||
2(k-
|
| a | ||
3+
|
a(
| ||
2(
|
∴|OM|2=(
| a | ||
|
a(
| ||
2(k-
|
| ||
| 6 |
| a2(1+k2) | ||
3(k-
|
|ON|2=(
| a | ||
3+
|
a(
| ||
2(
|
| ||
| 6 |
| a2(1+k2) | ||
3(
|
∴
| 1 |
| |OM|2 |
| 1 |
| |ON|2 |
| ||||||||
|
| 6(3+k2) |
| a2(1+k2) |
| 6 |
| a2 |
| 2 |
| 1+k2 |
∵-
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 2 |
| 1+k2 |
∴
| 15 |
| a2 |
| 6 |
| a2 |
| 2 |
| 1+k2 |
| 18 |
| a2 |
∴
| 1 |
| OM2 |
| 1 |
| ON2 |
| 18 |
| a2 |
| 15 |
| a2 |
从图形上看:当MN∥BC时取得最小值,当MN与AC边上的中线重合时取得最大值.
点评:本题考查了正三角形的中心(重心)的性质、直线相交于直线方程的问题、两点间的距离公式、反比例函数的单调性等基础知识与基本方法,属于难题.

练习册系列答案
相关题目
在等边三角形ABC中,M、N、P分别为AB、AC、BC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所在二面角的余弦值为
,则直线AM与NP所成角的大小为( )
| 1 |
| 3 |
| A、90° | ||||
| B、60° | ||||
C、arccos
| ||||
D、arccos
|
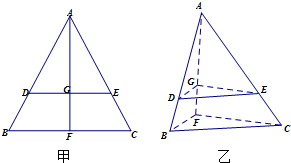 如图甲,在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC上的点,AF与DE交于点G,将△ABF沿AF折起,得到如图乙所示的三棱锥A-BCF,证明:DE∥平面BCF.
如图甲,在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC上的点,AF与DE交于点G,将△ABF沿AF折起,得到如图乙所示的三棱锥A-BCF,证明:DE∥平面BCF.