题目内容
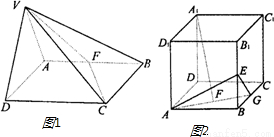
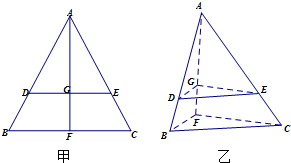如图甲，在等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC上的点，AF与DE交于点G，将△ABF沿AF折起，得到如图乙所示的三棱锥A-BCF，证明：DE∥平面BCF．分析：利用折叠前的线段比例关系怎么DE∥BC，折叠后利用线面平行证明面面平行，再由面面平行的性质得线面平行．
解答：
证明：∵折叠前，AD=AE，AB=AC，
=
，∴DE∥BC，
折叠后，DG∥BF，EG∥FC，
又DG，EG?平面BCF，BF，FC?平面BCF，
∴DG∥平面BCF，EG∥平面BCF，DG∩GE=G，
∴平面DEG∥平面BCF，DE?平面DEG，
∴DE∥平面BCF．
证明：∵折叠前，AD=AE，AB=AC，| AD |
| AB |
| AE |
| AC |
折叠后，DG∥BF，EG∥FC，
又DG，EG?平面BCF，BF，FC?平面BCF，
∴DG∥平面BCF，EG∥平面BCF，DG∩GE=G，
∴平面DEG∥平面BCF，DE?平面DEG，
∴DE∥平面BCF．
点评：本题考查了平行线分线段成比例定理，考查了线面的判定定理，面面平行的判定定理及面面平行的性质，其关键是证明面面平行．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=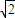
：1，F是AB的中点．
，
．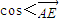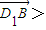