题目内容
（2011•许昌一模）在等边三角形ABC中，M、N、P分别为AB、AC、BC的中点，沿MN将△AMN折起，使得面AMN与面MNCB所成的二面角的余弦值为
，则直线AM与NP所成角α应满足
| 1 | 3 |
60°
60°
．分析：取MN的中点O，连接AO，OP，则cos∠AOP=
，求出AP，确定∠AMB（或其补角）是直线AM与NP所成角α，即可得到结论．
| 1 |
| 3 |
解答：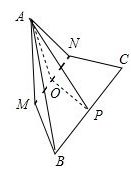
解：设等边三角形ABC的边长为4，取MN的中点O，连接AO，OP，则cos∠AOP=
∵AO=OP=
∴AP=
=2
连接NP，则
∵N、P分别为AAC、BC的中点，∴NP∥MB
∴∠AMB（或其补角）是直线AM与NP所成角α
∵AM=MB=2
∴∠AMB=60°
故答案为：60°
解：设等边三角形ABC的边长为4，取MN的中点O，连接AO，OP，则cos∠AOP=| 1 |
| 3 |
∵AO=OP=
| 3 |
∴AP=
AO2+PO2-2AO•PO•
|
连接NP，则
∵N、P分别为AAC、BC的中点，∴NP∥MB
∴∠AMB（或其补角）是直线AM与NP所成角α
∵AM=MB=2
∴∠AMB=60°
故答案为：60°
点评：本题考查空间角，考查余弦定理的运用，考查学生的计算能力，确定空间角是关键．
练习册系列答案
相关题目
（2011•许昌一模）如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点，
（2011•许昌一模）若某几何体的三视图（单位：cm）如图所示，则此几何体的表面积为（ ）