题目内容
(本小题满分12分)设 若
若
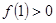 ,求证:
,求证:
(Ⅰ) 且
且 ;
;
(Ⅱ)方程 在
在 内有两个实根.
内有两个实根.
【答案】
(Ⅰ)因为 ,所以
,所以 .
.
由条件 ,消去
,消去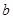 ,得
,得 ;
;
由条件 ,消去
,消去 ,得
,得 ,
, .
.
故 .
……6分
.
……6分
(Ⅱ)函数 的顶点坐标为
的顶点坐标为 ,
,
在 的两边乘以
的两边乘以 ,得
,得 .
.
又因为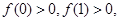 而
而
又因为 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以方程 在区间
在区间 与
与 内分别各有一实根。
内分别各有一实根。
故方程 在
在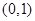 内有两个实根.
……12分
内有两个实根.
……12分
【解析】略

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目