题目内容
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,表面积最大的圆柱的底面半径是
.
| 3R |
| 4 |
| 3R |
| 4 |
分析:设内接圆柱的底面半径为r、高为h、全面积为S,利用比例线段求出h=3R-3r,从而将全面积表示成底面半径r的函数,利用二次函数的性质加以计算,可得答案.
解答:解:设内接圆柱的底面半径为r、高为h、全面积为S,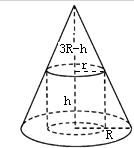
可得
=
,解之得h=3R-3r
∴S=2πrh+2πr2=2πr(3R-3r)+2πr2
=-4πr2+6πRr=-4π(r2-
Rr)
=-4π(r-
R)2+
πR2
∴当r=
时,S有最大值
πR2.
即圆锥的所有内接圆柱中,表面积最大的圆柱的底面半径是
.
故答案为:

可得
| 3R-h |
| 3R |
| r |
| R |
∴S=2πrh+2πr2=2πr(3R-3r)+2πr2
=-4πr2+6πRr=-4π(r2-
| 3 |
| 2 |
=-4π(r-
| 3R |
| 4 |
| 9 |
| 4 |
∴当r=
| 3R |
| 4 |
| 9 |
| 4 |
即圆锥的所有内接圆柱中,表面积最大的圆柱的底面半径是
| 3R |
| 4 |
故答案为:
| 3R |
| 4 |
点评:本题给出特殊的圆锥,求它的内接圆柱表面积的最大值.着重考查了圆锥的性质、圆柱的表面积计算和比例线段的计算等知识,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A、2πR2 | ||
B、
| ||
C、
| ||
D、
|
已知圆锥的底面半径为3,母线长为12,那么圆锥侧面展开图所成扇形的圆心角为( )
| A、180° | B、120° | C、90° | D、135° |