题目内容
11.已知函数f(x)=sinωx(ω>0)在区间[$-\frac{π}{3},\frac{π}{4}$]上的最小值是-1,则ω的最小值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 由题意可得函数的四分之一周期小于等于$\frac{π}{3}$,由周期公式可得ω的不等式,解不等式可得.
解答 解:∵函数f(x)=sinωx(ω>0)在区间[$-\frac{π}{3},\frac{π}{4}$]上的最小值是-1,
∴只要函数的四分之一周期小于等于$\frac{π}{3}$即可,即$\frac{2π}{4ω}$≤$\frac{π}{3}$,
解得ω≥$\frac{3}{2}$,∴ω的最小值为$\frac{3}{2}$.
故选:B.
点评 本题考查三角函数的最值和周期性,属基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
1.抛物线x2=-2y的焦点坐标是( )
| A. | (-1,0) | B. | (1,0) | C. | $(0,-\frac{1}{2})$ | D. | $(0,\frac{1}{2})$ |
1.以下说法正确的是( )
| A. | 命题“若x>1,则x2>1”的逆命题是“若x≤1,则x2≤1” | |
| B. | 命题:“?x0∈R,使得2+sinx0=0”的否定是“?x∈R,都有2+sinx≠0” | |
| C. | “x=1”是“x2-3x+2=0”的充要条件 | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
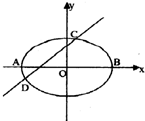 已知抛物线y2=4$\sqrt{2}$x的交点为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点.
已知抛物线y2=4$\sqrt{2}$x的交点为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点.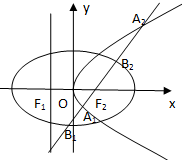 设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为$\frac{1}{2}$的椭圆记作C2
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为$\frac{1}{2}$的椭圆记作C2