题目内容
某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立.又知电梯只在有人下时才停止.(I)求某乘客在第i层下电梯的概率(i=2,3,4,5);
(Ⅱ)求电梯在第2层停下的概率;
(Ⅲ)求电梯停下的次数ξ的数学期望.
【答案】分析:(Ⅰ)由题意知本题是一个古典概型,试验发生的所有事件数共有4种结果,而满足条件的只有一个结果,根据古典概型公式得到结果.
(2)由第一问知一个乘客在某一层下的概率是 ,有4个乘客相当于发生4次独立重复试验,电梯在第2层停下的对立事件是都不在第二层下,不在某一层下的概率是1-
,有4个乘客相当于发生4次独立重复试验,电梯在第2层停下的对立事件是都不在第二层下,不在某一层下的概率是1- .
.
(3)某大楼共5层,4个人从第一层上电梯,可能在第五、第四、第三、第二层停,所以ξ可取1、2、3、4四种值,当ξ=1时表示电梯在整个过程中只停一次,又变为古典概型.
解答:解:(Ⅰ)由题意知本题是一个古典概型,
试验发生的所有事件数共有4种结果,
而满足条件的只有一个结果,
∴P= .
.
(Ⅱ)由第一问知一个乘客在某一层下的概率是 ,
,
有4个乘客相当于发生4次独立重复试验,
电梯在第2层停下的对立事件是都不在第二层下,
∴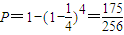
(Ⅲ)由题意知ξ可取1、2、3、4四种值,
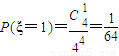 ;
;
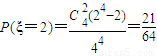 ;
;
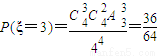 ;
;
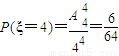
故ξ的分别列如下表:

∴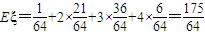
点评:期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,为今后学习数学及相关学科产生深远的影响.
(2)由第一问知一个乘客在某一层下的概率是
 ,有4个乘客相当于发生4次独立重复试验,电梯在第2层停下的对立事件是都不在第二层下,不在某一层下的概率是1-
,有4个乘客相当于发生4次独立重复试验,电梯在第2层停下的对立事件是都不在第二层下,不在某一层下的概率是1- .
.(3)某大楼共5层,4个人从第一层上电梯,可能在第五、第四、第三、第二层停,所以ξ可取1、2、3、4四种值,当ξ=1时表示电梯在整个过程中只停一次,又变为古典概型.
解答:解:(Ⅰ)由题意知本题是一个古典概型,
试验发生的所有事件数共有4种结果,
而满足条件的只有一个结果,
∴P=
 .
.(Ⅱ)由第一问知一个乘客在某一层下的概率是
 ,
,有4个乘客相当于发生4次独立重复试验,
电梯在第2层停下的对立事件是都不在第二层下,
∴
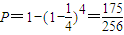
(Ⅲ)由题意知ξ可取1、2、3、4四种值,
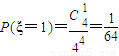 ;
;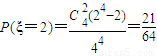 ;
;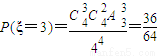 ;
;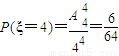
故ξ的分别列如下表:

∴
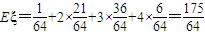
点评:期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,为今后学习数学及相关学科产生深远的影响.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
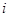 层下电梯的概率
层下电梯的概率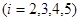 ;
; 的数学期望.
的数学期望.