题目内容
某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立.又知电梯只在有人下时才停止.(I)求某乘客在第i层下电梯的概率(i=2,3,4,5);
(Ⅱ)求电梯在第2层停下的概率;
(Ⅲ)求电梯停下的次数ξ的数学期望.
分析:(Ⅰ)由题意知本题是一个古典概型,试验发生的所有事件数共有4种结果,而满足条件的只有一个结果,根据古典概型公式得到结果.
(2)由第一问知一个乘客在某一层下的概率是
,有4个乘客相当于发生4次独立重复试验,电梯在第2层停下的对立事件是都不在第二层下,不在某一层下的概率是1-
.
(3)某大楼共5层,4个人从第一层上电梯,可能在第五、第四、第三、第二层停,所以ξ可取1、2、3、4四种值,当ξ=1时表示电梯在整个过程中只停一次,又变为古典概型.
(2)由第一问知一个乘客在某一层下的概率是
| 1 |
| 4 |
| 1 |
| 4 |
(3)某大楼共5层,4个人从第一层上电梯,可能在第五、第四、第三、第二层停,所以ξ可取1、2、3、4四种值,当ξ=1时表示电梯在整个过程中只停一次,又变为古典概型.
解答:解:(Ⅰ)由题意知本题是一个古典概型,
试验发生的所有事件数共有4种结果,
而满足条件的只有一个结果,
∴P=
.
(Ⅱ)由第一问知一个乘客在某一层下的概率是
,
有4个乘客相当于发生4次独立重复试验,
电梯在第2层停下的对立事件是都不在第二层下,
∴P=1-(1-
)4=
(Ⅲ)由题意知ξ可取1、2、3、4四种值,
P(ξ=1)=
=
;
P(ξ=2)=
=
;
P(ξ=3)=
=
;
P(ξ=4)=
=
故ξ的分别列如下表:

∴Eξ=
+2×
+3×
+4×
=
试验发生的所有事件数共有4种结果,
而满足条件的只有一个结果,
∴P=
| 1 |
| 4 |
(Ⅱ)由第一问知一个乘客在某一层下的概率是
| 1 |
| 4 |
有4个乘客相当于发生4次独立重复试验,
电梯在第2层停下的对立事件是都不在第二层下,
∴P=1-(1-
| 1 |
| 4 |
| 175 |
| 256 |
(Ⅲ)由题意知ξ可取1、2、3、4四种值,
P(ξ=1)=
| ||
| 44 |
| 1 |
| 64 |
P(ξ=2)=
| ||
| 44 |
| 21 |
| 64 |
P(ξ=3)=
| ||||||
| 44 |
| 36 |
| 64 |
P(ξ=4)=
| ||
| 44 |
| 6 |
| 64 |
故ξ的分别列如下表:

∴Eξ=
| 1 |
| 64 |
| 21 |
| 64 |
| 36 |
| 64 |
| 6 |
| 64 |
| 175 |
| 64 |
点评:期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,为今后学习数学及相关学科产生深远的影响.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
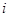 层下电梯的概率
层下电梯的概率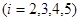 ;
; 的数学期望.
的数学期望.