题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(1)求角B的大小;
(2)已知函数y=cos2 +sin2
+sin2 -1,求y的取值范围.
-1,求y的取值范围.
解:(1)由(2a-c)cosB=bcosC,得(2sinA-sinC)cosB=sinBcosC,∴2sinAcosB=sin(B+C)=sinA.
∵0<A<π,∴sinA≠0,∴cosB= ,∵0<B<π,∴B=
,∵0<B<π,∴B= .
.
(2)∵B= ,∴A+C=
,∴A+C= ,∴函数y=cos2
,∴函数y=cos2 +sin2
+sin2 -1=
-1=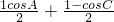 -1
-1
= [cosA-cos(
[cosA-cos(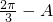 )]=
)]= (
( cosA-
cosA- sinA)=
sinA)= cos(
cos( +A).
+A).
∵0<A< ,∴
,∴ <(
<( +A)<
+A)< ,-
,- <cos(
<cos( +A)<
+A)< ,
,
∴- <y<
<y< .
.
分析:(1)由题意可得(2sinA-sinC)cosB=sinBcosC,cosB= ,根据0<B<π,可得 B=
,根据0<B<π,可得 B= .
.
(2)化简函数y= cos(
cos( +A),根据 0<A<
+A),根据 0<A< ,可得
,可得  <(
<( +A)<
+A)< ,从而求得cos(
,从而求得cos( +A) 的范围,
+A) 的范围,
即可求得y的范围.
点评:本题考查正弦定理的应用,同角三角函数的基本关系,余弦汗水due值域,化简函数y= cos(
cos( +A),是解题的
+A),是解题的
关键.
∵0<A<π,∴sinA≠0,∴cosB=
 ,∵0<B<π,∴B=
,∵0<B<π,∴B= .
.(2)∵B=
 ,∴A+C=
,∴A+C= ,∴函数y=cos2
,∴函数y=cos2 +sin2
+sin2 -1=
-1=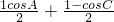 -1
-1 =
 [cosA-cos(
[cosA-cos(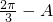 )]=
)]= (
( cosA-
cosA- sinA)=
sinA)= cos(
cos( +A).
+A).∵0<A<
 ,∴
,∴ <(
<( +A)<
+A)< ,-
,- <cos(
<cos( +A)<
+A)< ,
,∴-
 <y<
<y< .
.分析:(1)由题意可得(2sinA-sinC)cosB=sinBcosC,cosB=
 ,根据0<B<π,可得 B=
,根据0<B<π,可得 B= .
.(2)化简函数y=
 cos(
cos( +A),根据 0<A<
+A),根据 0<A< ,可得
,可得  <(
<( +A)<
+A)< ,从而求得cos(
,从而求得cos( +A) 的范围,
+A) 的范围,即可求得y的范围.
点评:本题考查正弦定理的应用,同角三角函数的基本关系,余弦汗水due值域,化简函数y=
 cos(
cos( +A),是解题的
+A),是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |