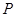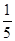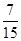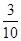Question

（本小题满分12分）

已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球，现从甲、乙两个盒内各任取2个球.

（Ⅰ）求取出的4个球中恰有1个红球的概率；

（Ⅱ）设“从甲盒内取出的2个球恰有1个为黑球”为事件A；“从乙盒内取出的2个球都是黑球”为事件B，求在事件A发生的条件下，事件B发生的概率；

（Ⅲ）设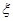为取出的4个球中红球的个数，求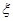的分布列和数学期望。

 

Answer 1

【答案】

（Ⅰ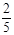）；（Ⅱ）；（Ⅲ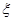）的分布列为

	0	1	2	3

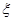 的数学期望。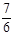

【解析】

试题分析：（Ⅰ）设“从甲盒内取出的2个球均为黑球；从乙盒内取出的2个球中，1个是红球，1个是黑球”为事件C，“从甲盒内取出的2个球中，1个是红球，1个是黑球；从乙盒内取出的2个球均为黑球”为事件D.由于事件C、D互斥，

则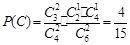,  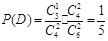   .………………… 3分

所以取出的4个球中恰有1个红球的概率为

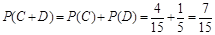.  ……………………………… 4分

（Ⅱ）解法一：由题可知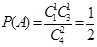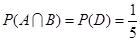，，则

。……………… 8分

解法二：由于事件A、B相互独立，故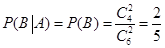。……………… 8分

（Ⅲ）设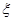可能的取值为0,1,2,3.

由（Ⅰ）、（Ⅱ）得, ,.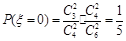

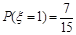所以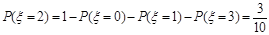. ………………… 11分

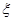∴的分布列为

	0	1	2	3

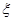∴ 的数学期望 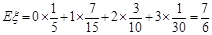……… 12分

考点：离散型随机变量的期望与方差；等可能事件的概率。

点评：本题主要考查等可能事件的概率与条件概率，以及离散型随机变量的分布列、期望与方差等知识点，属于中档题型，高考命题的趋向．分布列的求解应注意以下几点：（1）弄清随机变量每个取值对应的随机事件；（2）计算必须准确无误；（3）注意用分布列的两条性质检验所求的分布列是否正确。