题目内容
已知向量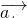
 .
. .
. .及实数x,y满足|
.及实数x,y满足| |=|
|=| |=1,
|=1, =
= +(x-3)
+(x-3) ,
,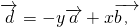 若
若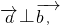
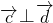 且
且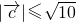 .
.
(1)求y关于x的函数关系 y=f(x)及其定义域.
(2)若x∈(1、6)时,不等式f(x)≥mx-16恒成立,求实数m的取值范围.
解:(1)∵ ,∴
,∴ ,又
,又
∴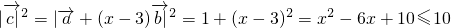
∴0≤x≤6
又∴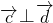 ,∴
,∴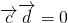 ,而∵
,而∵
∴y=x2-3x(0≤x≤6)
(2)若x∈(1,6)时,则使f(x)≥mx-16恒成立,
即使x2-3x≥mx-16恒成立,也就是: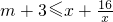 成立.
成立.
令: 在区间[0,4]递减,在区间[4,+∞]递增,
在区间[0,4]递减,在区间[4,+∞]递增,
∴当x∈(1,6)时,g(x)min=g(4)=8∴m+3≤8即m≤5
分析:(1)由 及
及 可求
可求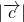 ,结合
,结合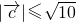 可求x的取值范围,然后由
可求x的取值范围,然后由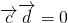 代入可求y与x之间的关系
代入可求y与x之间的关系
(2)由x∈(1,6)时,则使f(x)≥mx-16恒成立,整理可得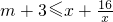 成立,构造函数
成立,构造函数 ,通过研究函数g(x)在区间x∈(1,6)上单调性可求函数g(x)的最小值,从而可求m的取值范围
,通过研究函数g(x)在区间x∈(1,6)上单调性可求函数g(x)的最小值,从而可求m的取值范围
点评:本题以平面向量的基本运输为载体,考查了向量数量积的性质,函数恒成立问题的转化及利用单调性求解函数的最值,体现了转化思想在解题中的应用.
 ,∴
,∴ ,又
,又
∴
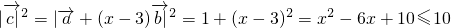
∴0≤x≤6
又∴
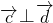 ,∴
,∴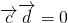 ,而∵
,而∵
∴y=x2-3x(0≤x≤6)
(2)若x∈(1,6)时,则使f(x)≥mx-16恒成立,
即使x2-3x≥mx-16恒成立,也就是:
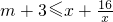 成立.
成立.令:
 在区间[0,4]递减,在区间[4,+∞]递增,
在区间[0,4]递减,在区间[4,+∞]递增,∴当x∈(1,6)时,g(x)min=g(4)=8∴m+3≤8即m≤5
分析:(1)由
 及
及 可求
可求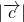 ,结合
,结合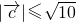 可求x的取值范围,然后由
可求x的取值范围,然后由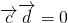 代入可求y与x之间的关系
代入可求y与x之间的关系(2)由x∈(1,6)时,则使f(x)≥mx-16恒成立,整理可得
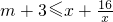 成立,构造函数
成立,构造函数 ,通过研究函数g(x)在区间x∈(1,6)上单调性可求函数g(x)的最小值,从而可求m的取值范围
,通过研究函数g(x)在区间x∈(1,6)上单调性可求函数g(x)的最小值,从而可求m的取值范围点评:本题以平面向量的基本运输为载体,考查了向量数量积的性质,函数恒成立问题的转化及利用单调性求解函数的最值,体现了转化思想在解题中的应用.

练习册系列答案
相关题目