题目内容
17.已知b是实数,若$\frac{1+bi}{2-i}$是纯虚数,则b=( )| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 利用复数的运算法则、纯虚数的定义即可得出.
解答 解:∵$\frac{1+bi}{2-i}$=$\frac{(1+bi)(2+i)}{(2-i)(2+i)}$=$\frac{2-b+(1+2b)i}{5}$是纯虚数,
则b=$\left\{\begin{array}{l}{\frac{2-b}{5}=0}\\{\frac{1+2b}{5}≠0}\end{array}\right.$,解得b=2.
故选:A.
点评 本题考查了复数的运算法则、纯虚数的定义,考查了计算能力,属于基础题.

练习册系列答案
相关题目
9.已知函数f(x)=sinx+2$\sqrt{3}$cos2$\frac{x}{2}$,设a=f($\frac{π}{7}$),b=f($\frac{π}{6}$),c=f($\frac{π}{3}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
6.已知f(x)=ax2+bx+c,(a>0),若f(-1)=f(3),则f(-1),f(1),f(4)的大小关系为 ( )
| A. | f(-1)<f(1)<f(4) | B. | f(1)<f(-1)<f(4) | C. | f(-1)<f(4)<f(1) | D. | f(4)<f(-1)<f(1) |
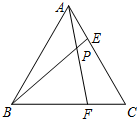 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P. 在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).
在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).