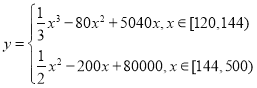题目内容
【题目】已知![]() .
.
(1)当![]() 为何值时,
为何值时, ![]() 最小? 此时
最小? 此时![]() 与
与![]() 的位置关系如何?
的位置关系如何?
(2)当![]() 为何值时,
为何值时, ![]() 与
与![]() 的夹角最小? 此时
的夹角最小? 此时![]() 与
与![]() 的位置关系如何?
的位置关系如何?
【答案】(1) 当![]() 时,
时, ![]() 最小,
最小, ![]() ;(2)
;(2)![]() 时,
时, ![]() 与
与![]() 的夹角最小,
的夹角最小, ![]() 与
与![]() 平行.
平行.
【解析】试题分析:(1)由向量的坐标运算,可将![]() 表示成关于
表示成关于![]() 的二次函数,利用二次函数的最值求得
的二次函数,利用二次函数的最值求得![]() 何时求最小值.由
何时求最小值.由![]() 求得
求得![]() ,进一步可得两者位置关系;(2)由
,进一步可得两者位置关系;(2)由![]() 的坐标运算,转化为关于
的坐标运算,转化为关于![]() 的表达式,由夹角最小时,余弦值最大为
的表达式,由夹角最小时,余弦值最大为![]() ,可得关于
,可得关于![]() 的方程,解得
的方程,解得![]() ,再求得此时
,再求得此时![]() 与
与![]() 的坐标,可判断两者的位置关系.
的坐标,可判断两者的位置关系.
试题解析:
(1)![]() ,
,
![]()
![]()
当![]() 时,
时, ![]() 最小,此时
最小,此时![]() ,
,![]() , ∴
, ∴![]()
∴当![]() 时,
时, ![]() 最小,此时
最小,此时![]() .
.
(2)设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() ,
,
要![]() 与
与![]() 的夹角最小,则
的夹角最小,则![]() 最大, ∵
最大, ∵![]() ,故
,故![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,
,
![]() ,解之得
,解之得![]() ,
,![]() .
.
∴![]() 时,
时, ![]() 与
与![]() 的夹角最小, 此时
的夹角最小, 此时![]() 与
与![]() 平行.
平行.

练习册系列答案
相关题目