题目内容
已知函数
是定义在
上的偶函数，并满足
，当
时，
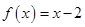，则
-1
解析试题分析：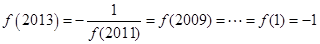
。
考点：函数的奇偶性
点评：本题提供的是时函数的解析式，因而需要将
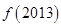中x的值2013化在的范围内。
练习册系列答案
相关题目
题目内容
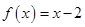已知函数是定义在上的偶函数，并满足，当时，，则
-1
解析试题分析：。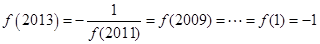
考点：函数的奇偶性
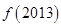点评：本题提供的是时函数的解析式，因而需要将中x的值2013化在的范围内。
，其中
，若动直线
与函数
的图像有三个不同的交点，它们的横坐标分别为
，
的取值范围是_______________.
是否存在最大值？若存在，在横线处填写其最大值；若不存在，直接填写“不存在”_______________.
的定义域为______
的定义域是_ ____．
上的偶函数
，且对任意实数
都有
，当
时，
，若在区间
内，函数
有4个零点，则实数
的取值范围是 ．
的定义域为 .
，有下列结论：①函数
的定义域是（0，+∞）；②函数
；④当
时，函数
时，函数
，满足
，若
，
，则集合
中最小的元素是 .
是奇函数，且在区间
上是单调增函数，又
，则
的解集为 .