题目内容
关于函数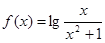 ,有下列结论:①函数
,有下列结论:①函数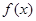 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数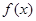 是奇函数;③函数
是奇函数;③函数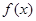 的最小值为-
的最小值为-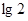 ;④当
;④当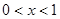 时,函数
时,函数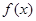 是增函数;当
是增函数;当 时,函数
时,函数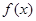 是减函数.
是减函数.
其中正确结论的序号是 .(写出所有你认为正确的结论的序号)
①③④
解析试题分析:由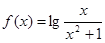 知
知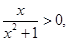 所以,x>0,即①函数
所以,x>0,即①函数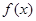 的定义域是(0,+∞),正确。
的定义域是(0,+∞),正确。
②函数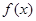 是奇函数,不正确,定义域不关于原点对称。
是奇函数,不正确,定义域不关于原点对称。
因为,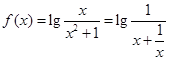 ,
,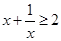 ,所以,③函数
,所以,③函数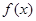 的最小值为-
的最小值为-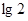 ,正确。
,正确。
由“对号函数”的单调性及复合函数的单调性,④当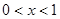 时,函数
时,函数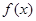 是增函数;当
是增函数;当 时,函数
时,函数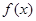 是减函数.正确,综上知答案为①③④。
是减函数.正确,综上知答案为①③④。
考点:复合函数的单调性,对数函数的性质,函数的奇偶性,均值定理的应用。
点评:中档题,本题以复合对数函数为研究对象,较全面考察函数的定义域、函数的奇偶性及函数的单调性,均值定理的应用。

练习册系列答案
相关题目
 为偶函数,那么
为偶函数,那么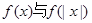 的大小关系为 __.
的大小关系为 __.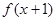 的定义域为
的定义域为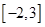 ,则
,则 的定义域是 。
的定义域是 。  是定义在
是定义在 上的偶函数,并满足
上的偶函数,并满足 ,当
,当 时,
时,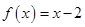 ,则
,则
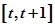 上满足不等式
上满足不等式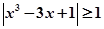 的解有且只有一个,则实数
的解有且只有一个,则实数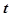 的取值范围是_________。
的取值范围是_________。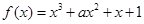 在(0,3)内递增,则实数
在(0,3)内递增,则实数 的取值范围是_________
的取值范围是_________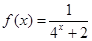 ,利用课本中推导等差数列前
,利用课本中推导等差数列前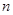 项和公式的方法,可求得
项和公式的方法,可求得 的值是________________;
的值是________________; 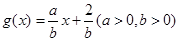 和函数
和函数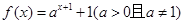 的图象恒过同一个定点,则
的图象恒过同一个定点,则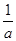 +
+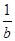 的最小值为________.
的最小值为________. 为一次函数,且
为一次函数,且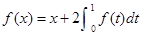 ,则
,则