题目内容
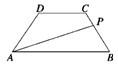 等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.
分析:(1)先作出所需辅助线:过C点作CE⊥AB于E,再分类讨论求出:在当x∈(0,5]时,当x∈(5,9]时,当x∈(9,14]时,函数S=f(x)表达式即可;
(2)分类讨论:当x∈(0,5]时,当x∈(5,9]时,当x∈(9,14]时,分别求出各个区间上的最大值,最后综合即得,△ABP的面积S最大值即可.
(2)分类讨论:当x∈(0,5]时,当x∈(5,9]时,当x∈(9,14]时,分别求出各个区间上的最大值,最后综合即得,△ABP的面积S最大值即可.
解答: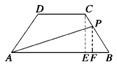 解(1)过C点作CE⊥AB于E,
解(1)过C点作CE⊥AB于E,
在△BEC中,CE=
=4,∴sinB=
.
由题意,当x∈(0,5]时,过P点作PF⊥AB于F,
∴PF=xsinB=
x,∴S=
×10×
x=4x,
当x∈(5,9]时,∴S=
×10×4=20.
当x∈(9,14]时,AP=14-x,PF=AP•sinA=
,
∴S=
×10×(14-x)×
=56-4x.综上可知,
函数S=f(x)=
(2)由(1)知,当x∈(0,5]时,f(x)=4x为增函数,
所以,当x=5时,取得最大值20.
当x∈(5,9]时,f(x)=20,最大值为20.当x∈(9,14]时,f(x)=56-4x为减函数,无最大值.
综上可知:当P点在CD上时,△ABP的面积S最大为20.
 解(1)过C点作CE⊥AB于E,
解(1)过C点作CE⊥AB于E,在△BEC中,CE=
| 52-32 |
| 4 |
| 5 |
由题意,当x∈(0,5]时,过P点作PF⊥AB于F,
∴PF=xsinB=
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
当x∈(5,9]时,∴S=
| 1 |
| 2 |
当x∈(9,14]时,AP=14-x,PF=AP•sinA=
| 4(14-x) |
| 5 |
∴S=
| 1 |
| 2 |
| 4 |
| 5 |
函数S=f(x)=
|
(2)由(1)知,当x∈(0,5]时,f(x)=4x为增函数,
所以,当x=5时,取得最大值20.
当x∈(5,9]时,f(x)=20,最大值为20.当x∈(9,14]时,f(x)=56-4x为减函数,无最大值.
综上可知:当P点在CD上时,△ABP的面积S最大为20.
点评:本小题主要函数模型的选择与应用.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
相关题目
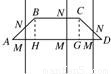
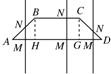 等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.
等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域. 如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.
如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.