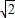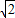题目内容
 如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.
如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.分析:由题目给出的已知条件求出HG的长度及BH的长度,然后根据M点的位置分别计算直线MN左侧图形的面积.最后列出分段函数解析式.
解答:解:∵四边形ABCD是等腰梯形,且AD=2,BC=1,∠BAD=45°,
知:GH=1,AH=GD=
,BH=CG=
.
当0<x≤
时,在△AMN中,∠MAN=45°,故MN=AM=x,∴y=
x2;
当
<x≤
时,y=
+(x-
)×
=
x-
;
当
<x≤2时,y=
(1+2)×
-(2-x)2×
=
-
(x-2)2.
故y与x的函数关系式为y=
函数的定义域为(0,2].
知:GH=1,AH=GD=
| 1 |
| 2 |
| 1 |
| 2 |
当0<x≤
| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
当
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
故y与x的函数关系式为y=
|
函数的定义域为(0,2].
点评:本题考查了函数解析式的求解及常用方法,体现了数学转化思想方法,考查了几何图形面积的求法,是基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
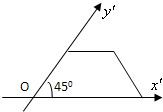 一梯形的直观图是一个如图所示的等腰梯形,且梯形OA′B′C′的面积为
一梯形的直观图是一个如图所示的等腰梯形,且梯形OA′B′C′的面积为| 2 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
 ,则原梯形的面积为(
)
,则原梯形的面积为(
)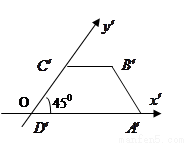
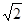 ,则原梯形的面积为( )
,则原梯形的面积为( ) 
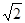 ,则原图形的面积为( )
,则原图形的面积为( ) 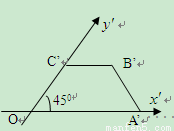
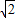 ,则原梯形的面积为( )
,则原梯形的面积为( )