题目内容
等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.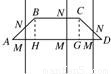
【答案】分析:直线MN左侧的面积的计算方法与MN所处的位置不同计算方式不同,MN所处的位置可分为三种情况:M在A,H之间,M在H,G之间或M在G,D之间,所以分三段计算求解.
解答:解析;作BH⊥AD,H为垂足,
CG⊥AD,G为垂足,
依题意,则有AH= ,AG=
,AG= a.
a.
(1)当M位于点H的左侧时,
N∈AB,由于AM=x,∠BAD=45°,
∴MN=x.
∴y=S△AMN= x2(0≤x≤
x2(0≤x≤ ).
).
(2)当M位于HG之间时,
由于AM=x,∠BAD=45°,
∴MN= ,BN=x-
,BN=x-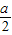 .
.
∴y=S直角梯形AMNB= •
• [x+(x-
[x+(x- )]=
)]= ax-
ax- (
( <x≤
<x≤ a).
a).
(3)当M位于点G的右侧时,
由于AM=x,MN=MD=2a-x,
∴y=S梯形ABCD-S△MDN= •
•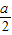 (2a+a)-
(2a+a)- (2a-x)2=
(2a-x)2=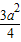 -
- (4a2-4ax+x2)=-
(4a2-4ax+x2)=- x2+2ax-
x2+2ax-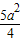 (
( a<x≤2a).
a<x≤2a).
综上: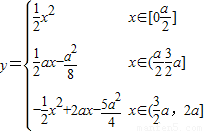
点评:本题属于一道分段函数的应用问题,属于一个中档题,能有效考查学生综合运用知识解决问题的能力.
解答:解析;作BH⊥AD,H为垂足,
CG⊥AD,G为垂足,
依题意,则有AH=
 ,AG=
,AG= a.
a.(1)当M位于点H的左侧时,
N∈AB,由于AM=x,∠BAD=45°,
∴MN=x.
∴y=S△AMN=
 x2(0≤x≤
x2(0≤x≤ ).
).(2)当M位于HG之间时,
由于AM=x,∠BAD=45°,
∴MN=
 ,BN=x-
,BN=x-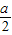 .
.∴y=S直角梯形AMNB=
 •
• [x+(x-
[x+(x- )]=
)]= ax-
ax- (
( <x≤
<x≤ a).
a).(3)当M位于点G的右侧时,
由于AM=x,MN=MD=2a-x,
∴y=S梯形ABCD-S△MDN=
 •
•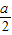 (2a+a)-
(2a+a)- (2a-x)2=
(2a-x)2=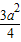 -
- (4a2-4ax+x2)=-
(4a2-4ax+x2)=- x2+2ax-
x2+2ax-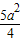 (
( a<x≤2a).
a<x≤2a).综上:
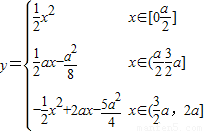
点评:本题属于一道分段函数的应用问题,属于一个中档题,能有效考查学生综合运用知识解决问题的能力.

练习册系列答案
相关题目
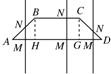 等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.
等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.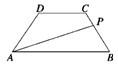 等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S 如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.
如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.